Worksheet 2B - Series Circuit Calculations - Solutions and Commentary
Question 1
The objective of this question is to work out the unknown voltage \( V \).
We have the following information:
- the resistances in the circuit; and
- the driving source current of the circuit (6 A).
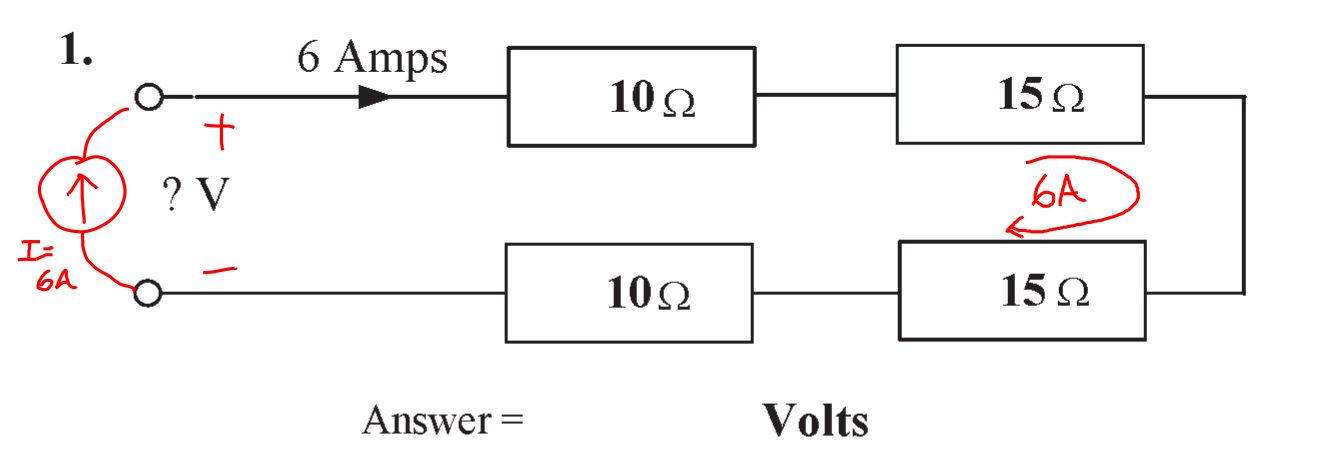
Two methods of solving this problem are shown below.
Method 1
Method 1 uses Ohm's Law on the total resistance \( R_{\mathrm{TOT}} \) of the circuit.
Before calculating the supply voltage \( V \), the total resistances must be calculated.
\( R_{\mathrm{TOT}} = \sum R = 2 \cdot (10 + 15) = 50 \), i.e. \( R_{\mathrm{TOT}} \) = 50 Ω.
This circuit may now be solved using Ohm's Law:
\( V = I R_{\mathrm{TOT}} = 6 \cdot 50 = 300 \) i.e. \( V \) = 300 V #.
Method 2
Method 2 computes the voltage drops across each individual resistor, then sums these voltages to get the supply voltage.
The computed voltages are as follows. Calculations are not repeated for identical value resistors subject to the same current flow.
- The voltage across drop across a 10 Ω resistor \( V_{10} = 6 \cdot 10 \) = 60 V; and
- The voltage across drop across a 15 Ω resistor \( V_{15} = 6 \cdot 15 \) = 90 V.
This circuit may now be solved by adding up the voltage drops across the resistors:
\( V = 2 \cdot (V_{10} + V_{15}) = 2 \cdot (60 + 90) = 300 \) i.e. \( V \) = 300 V #.
Question 2
The objective of this question is to work out the following quantities:
- The supply voltage \( V_{\mathrm{s}} \);
- The supply current \( I_{\mathrm{s}} \).
We have the following information:
- The resistances;
- The voltage drop across every resistance.
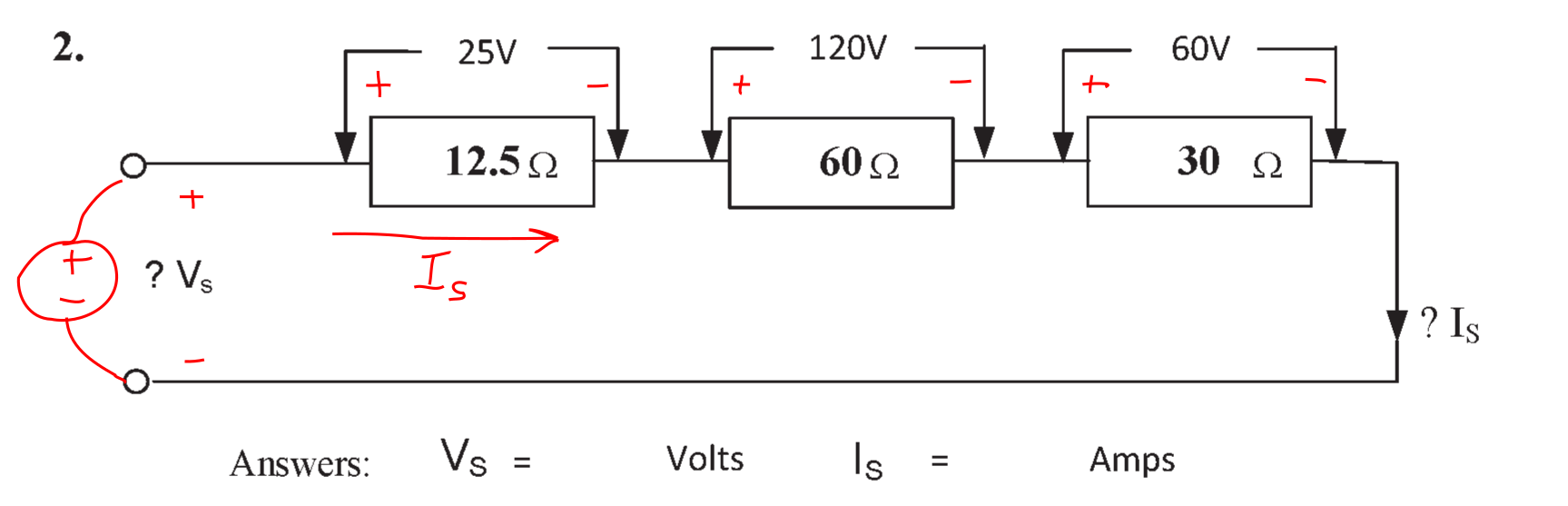
Some methods of solving this circuit are shown below.
In all cases, the following variables are used:
- \( V_{\mathrm{12.5}} \): the voltage drop across the 12.5 Ω resistor (25 V);
- \( V_{\mathrm{60}} \): the voltage drop across the 60 Ω resistor (120 V); and
- \( V_{\mathrm{30}} \): the voltage drop across the 30 Ω resistor (60 V).
Method 1
This method relies on the supply voltage being the sum of the voltage drops across each resistor i.e. \( V_{\mathrm{s}} = V_{12.5} + V_{60} + V_{30} \).
The supply voltage is calculated by adding up the individual resistor voltage drops.
\( V_{\mathrm{s}} = \sum V = V_{12.5} + V_{60} + V_{30} = 25 + 120 + 60 \) = 205 V #.
The supply current can be found by applying Ohm's Law to any of the resistors, since (i) all of the resistors have the supply current flowing through them; (ii) the voltage drop across them is known; and (iii) the resistance value is known.
NOTE: You only need to use one of these calculations to get your answer. However, the answers from each resistor should all yield the same result.
The three methods of calculating \( I_{\mathrm{s}} \) are:
- From the 12.5 Ω resistor: \( I_{\mathrm{s}} = \frac{ V_{12.5}}{12.5} = \frac{25}{12.5} \) = 2 A #;
- From the 60 Ω resistor: \( I_{\mathrm{s}} = \frac{ V_{60}}{60} = \frac{120}{60} \) = 2 A #;
- From the 25 Ω resistor: \( I_{\mathrm{s}} = \frac{ V_{25}}{25} = \frac{50}{25} \) = 2 A #.
These calculations all yield the same result, which is required for the circuit to be consistent.
Method 2
The series resistance method is similar to the KVL method except it uses the total resistance to calculate the supply voltage.
\( R_{\mathrm{TOT}} = \sum R = 12.5 + 60 + 30 = \) 102.5 Ω, i.e. \( R_{\mathrm{TOT}} \) = 102.5 Ω.
The supply voltage can then be calculated using KVL.
\( V_{\mathrm{s}} = \sum V = 25 + 120 + 60 \) = 205 V #.
The supply current can then be calculated from the supply voltage and the total resistance.
\( I_{\mathrm{s}} = \frac{V_{\mathrm{s}}}{R_{\mathrm{TOT}}} = \frac{205}{102.5} \) = 2 A #.
Question 3
The objective of this question is to work out the following quantities:
- The supply current \( I_{\mathrm{s}} \).
We have the following information:
- the circuit below.
- the desired supply voltages (\ V_{\mathrm{s}} \) of 5 V and 10 V.
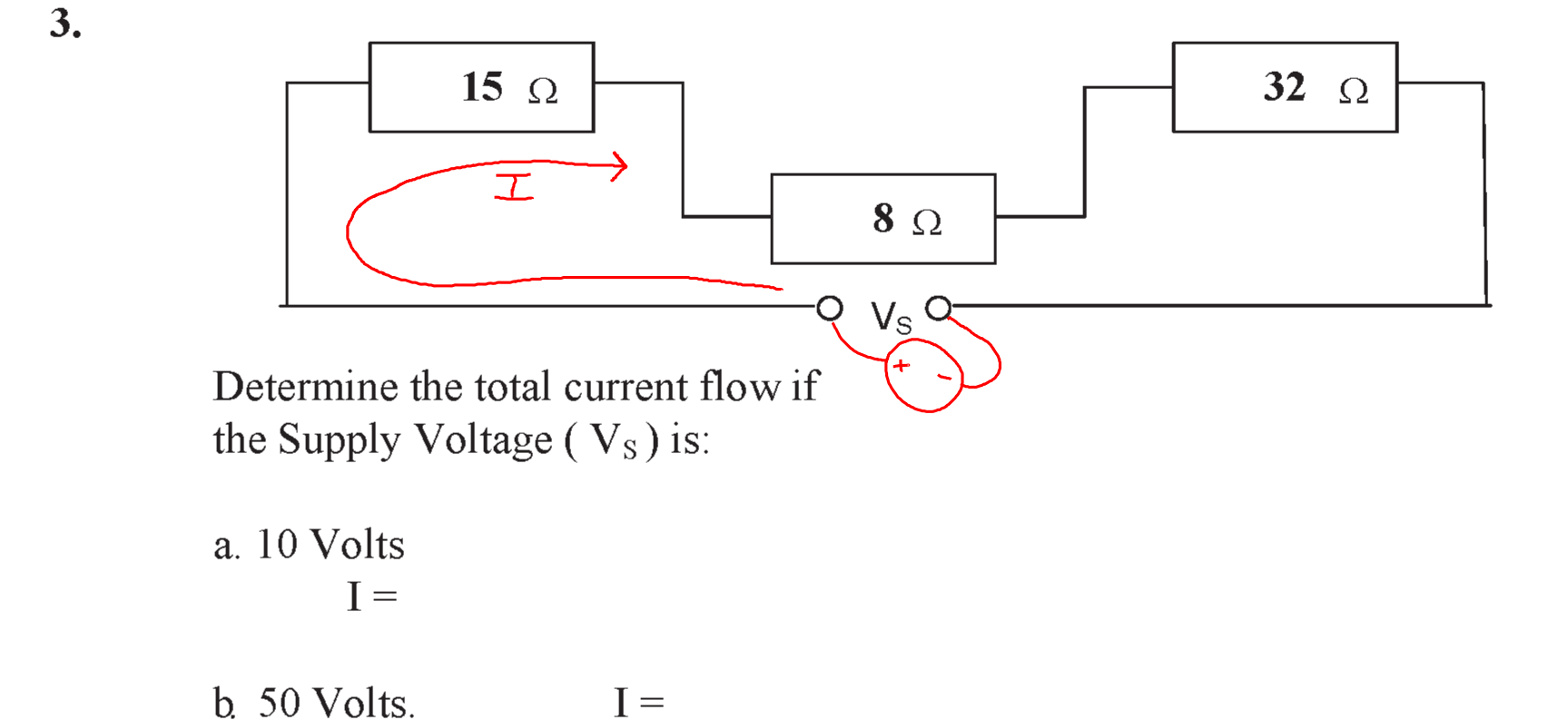
Method
The total resistance \( R_{\mathrm{TOT}} \) is required to calculate the supply current.
\( R_{\mathrm{TOT}} = \sum R = 15 + 8 + 32 = 55 \), i.e. \( R_{\mathrm{TOT}} \) = 55 Ω.
The supply current \( I_{\mathrm{s}} \) is calculated using Ohm's Law for each respective voltage using Ohm's Law. The equation used is \( I = \frac{V_{\mathrm{s}}}{R_{\mathrm{TOT}}} = \frac{V_{\mathrm{s}}}{55} \).
| \( V_{\mathrm{s}} \) (V) | \( I \) (A) |
|---|---|
| 5 | 0.0909 |
| 10 | 0.1818 |
Question 4
The objective of this question is to work out the following quantities:
- The supply current \( I_{\mathrm{s}} \);
- The voltage drop across each of the 25 Ω resistors connected in series.
We have the following information:
- the supply voltage is 100 V.

Method 1
Method 1 relies on voltage division, and using the total resistance \( R_{\mathrm{TOT}} \) to calculate the supply current.
\( R_{\mathrm{TOT}} = \sum R = 15 \cdot 4 = 60 \), i.e. \( R_{\mathrm{TOT}} \) = 60 Ω.
The supply current \( I_{\mathrm{s}} \) is calculated using Ohm's Law.
\( I_{\mathrm{s}} = \frac{100}{60} \) = 1.667 A (4 sf) #.
The voltage drops across the 15 Ω resistors are calculated using Voltage Division. The resistors are all the same value, and there are four of them, so the voltage drop across each resistor is \( \frac{1}{4} \) of the supply voltage.
- \( V_{15} = 100 \cdot \frac{1}{4} \) = 25 V #.
Method 2
The total resistance \( R_{\mathrm{TOT}} \) is used to calculate the supply current.
\( R_{\mathrm{TOT}} = \sum R = 15 \cdot 4 = 60 \), i.e. \( R_{\mathrm{TOT}} \) = 60 Ω.
The supply current \( I_{\mathrm{s}} \) is calculated using Ohm's Law.
\( I_{\mathrm{s}} = \frac{100}{60} \) = 1.6667 (5 sf) or 1.667 A (4 sf) #.
The voltage drops across the 15 Ω resistors are calculated using Ohm's Law.
- \( V_{15} =I_{\mathrm{s}} R = 15 \cdot 1.6667 \) = 25.00 V (4 sf) #.
This method is more prone to round-off error. That is why a five significant figure version of the current was kept for calculating \( V_{15} \).