Worksheet 3A - Series Circuit Calculations - Solutions and Commentary

Question 1

The objective of this question is to work out the unknown resistance \( R_4 \).

The circuit is shown below.

The information we have is:

• The supply voltage is 300 V.
• The supply current is 20 A.

Method 1

Method 1 uses Ohm's Law on the total resistance \( R_{\mathrm{TOT}} \) of the circuit, and from that deducing the "missing" resistance.

The total resistance is calculated from the supply voltage and supply current.

\( R_{\mathrm{TOT}} = \frac{300}{20} \) = 15 Ω.

The other resistances (R₁, R₂, and R₃) add up to 7 Ω.

Therefore, \( R_4 = R_{\mathrm{TOT}} - 7 \) = 8 Ω #.

Method 2

Method 2 computes the voltage drops across the known resistors, then uses the voltage drop across the unknown resistance and the current to solve for the unknown resistance.

The other resistances (R₁, R₂, and R₃) add up to 7 Ω. The voltage drop across this total resistance is 140 V at 20 A current flow.

The voltage across \( R_4 \) is therefore 300 - 140 = 160 V.

Therefore, \( R_4 = \frac{180}{20} \) = 8 Ω #.

Question 2

The objective of this question is to work out the following quantities:

• The resistance \( R_1 \);
• The resistance \( R_3 \);
• The voltage drop across \( R_4 \);
• The supply voltage \( V_{\mathrm{s}} \).

The circuit is shown below.

We have the following information:

• The current through all the resistors is 8 A.
• The voltage drop across \( R_1 \) is 12 V.
• The voltage drop across \( R_3 \) is 8 V.
• The resistance of \( R_4 \) is 16 Ω.

Solution

This circuit can be solved with Ohm's Law only.

The current through all of the resistors is 8 A, and all unknown resistors have a known voltage drop.

Therefore, the resistance may be calculated using \( R = \frac{V}{I} \).

The unknown resistance values are as follows:

• \( R_1 = \frac{12}{8} \) = 1.5 Ω #.
• \( R_3 = \frac{8}{8} \) = 1 Ω #.

The voltage across \( R_4 \) is also calculated using \( V = I R \).

• \( V_{\mathrm{R4}} = V_{4} = 8 \cdot 16 \) = 128 V #.

The supply voltage can be determined two main ways:

• Adding up the voltage drops across the resistors; or
• Adding up the resistances, and multiplying by the current.

Adding up the resistor voltage drops is the quickest as we already have three of them out of four.

It is also possible to use the total series resistance.

Question 3

The objective of this question is to work out the following quantities:

• The voltage drop across \( R_3 \) (\( V_{3} \)  or \( V_{\mathrm{R3}} \) );
  
• The voltage drop across \( R_5 \) (\( V_{5} \)  or \( V_{\mathrm{R5}} \) );
  
• The value of the unknown resistance \( R_6 \).

The circuit is shown below.

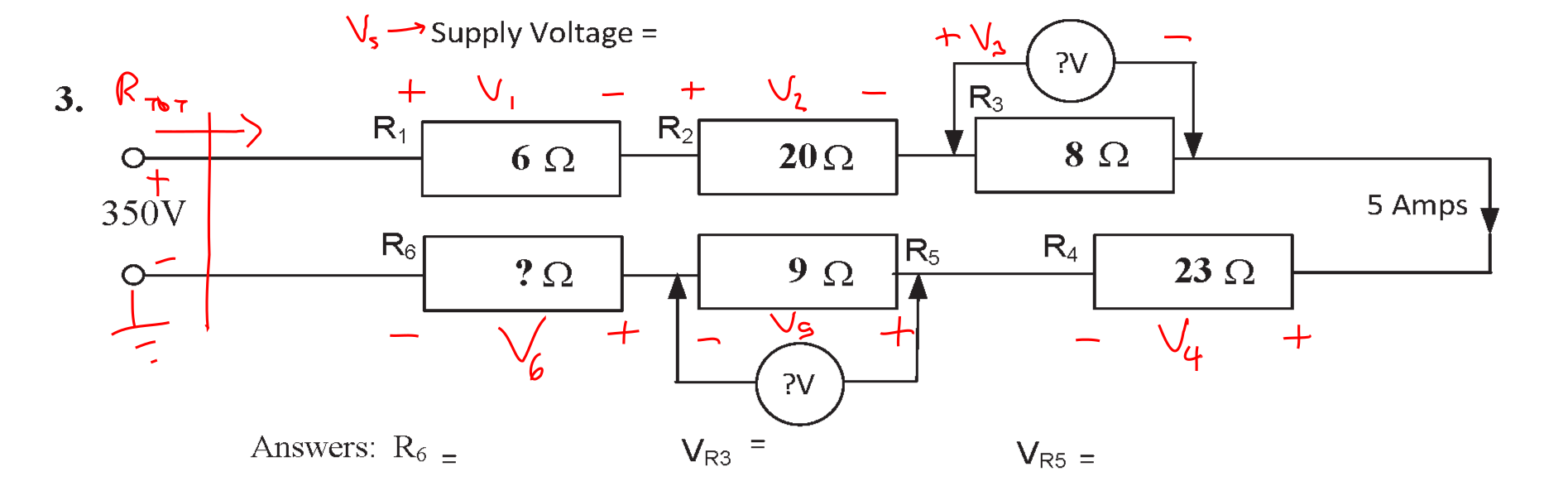
Method

The current through all the resistors is known to be 5 A.

We can calculate the voltage drops across \( R_3 \) and \( R_5 \) immediately.

• \( V_{\mathrm{R3}} = V_{3} = 5 \cdot 8 \) = 40 V #;
• \( V_{\mathrm{R5}} = V_{5} = 5 \cdot 9 \) = 45 V #.

We know that the supply voltage is 350 V, and the supply current is 5 A. Using Ohm's Law, the resistance of the circuit as seen by the driving source (whether the driving source is a 350 V voltage source or a 5 A current source) must be 70 Ω, i.e. \(R_{\mathrm{TOT}} \) = 70 Ω.

The resistors \( R_1 \) through \( R_5 \) total up to 66 Ω.

Resistance \( R_6 \) is the "remaining" resistance when 66 is subtracted from 70 i.e. \( R_6 \) = 4 Ω.

Question 4

The objective of this question is to work out the following quantities:

• The supply current \( I_{\mathrm{s}} \);
• The voltage drop across each of the 25 Ω resistors connected in series.

The circuit is shown below.

Solution

This question is more complicated than the previous ones because it is not initially possible to compute the driving source resistance.

The current in the circuit can be deduced from \( R_2 \) and \( V_2 \) by means of Ohm's Law.

\( I = \frac{10}{2} = 5\) A #.

Now we know that the voltage driving the circuit is 230 V, and the current is 5 A. The total resistance of the circuit is therefore 46 Ω.

Resistors \( R_1 \) through \( R_3 \) have a total resistance of 23 Ω.

Resistor \( R_4 \) is the "remaining" resistance required to make the total resistance 46 Ω.

\( R_4 = 46 - 23 \) = 23 Ω #.

Question 5

The objective of this question is to work out the following quantities:

• The voltage drop across \( R_3 \) (\( V_{3} \)  or \( V_{\mathrm{R3}} \) );
• The value of the unknown resistance \( R_1 \);
• The value of the unknown resistance \( R_3 \).

The circuit is shown below.

Solution

Resistance \( R_1 \) can be calculated immediately from the 2 A load current and 9 V voltage drop.

\( R_1 = \frac{9}{2} \) = 4.5 Ω #.

We know that the voltage driving the circuit is 50 V, and the current is 2 A. The total resistance of the circuit is therefore 25 Ω.

Resistors \( R_1 \), \( R_2 \) and \( R_4 \) have a total resistance of 22.5 Ω.

Resistor \( R_4 \) is the "remaining" resistance required to make the total resistance 25 Ω.

\( R_4 = 25 - 22.5 \) = 2.5 Ω #.