Worksheet 10D - Total Resistance Network - Solutions and Commentary
Question 1
The circuit is shown below.

Solution
The circuit may be solved by direct inspection.
The calculation of the total resistance \( R_{\mathrm{T}} \) is shown below.
\( R_{\mathrm{T}} = 14 + 7 + 24 + 19 + 6 \) = 70 Ω #.
Question 2
The circuit is shown below.

The resistors are grouped up into three groups 1-3.
The order of resistors in a series circuit does not matter, even if they are "separated" by parallel circuits.
Solution - Method 1
The total resistance \( R_{\mathrm{T}} \) is simply the sum of \( R_1 \), \( R_2 \) and \( R_3 \).
- \( R_1 = 14 + 7 + 19 \) = 40 Ω.
- \( R_2 = 24 \parallel 24 = \frac{24}{2} \) = 12 Ω.
- \( R_3 = 6 \parallel 6 = \frac{6}{2} \) = 3 Ω.
The new equivalent circuit is shown below.

The total resistance \( R_{\mathrm{T}} \) is simply the sum of the individual series resistors.
\( R_{\mathrm{T}} = R_1 + R_2 + R_3 = 40 + 12 + 3 \) = 55 Ω #.
Question 3
The circuit is shown below.
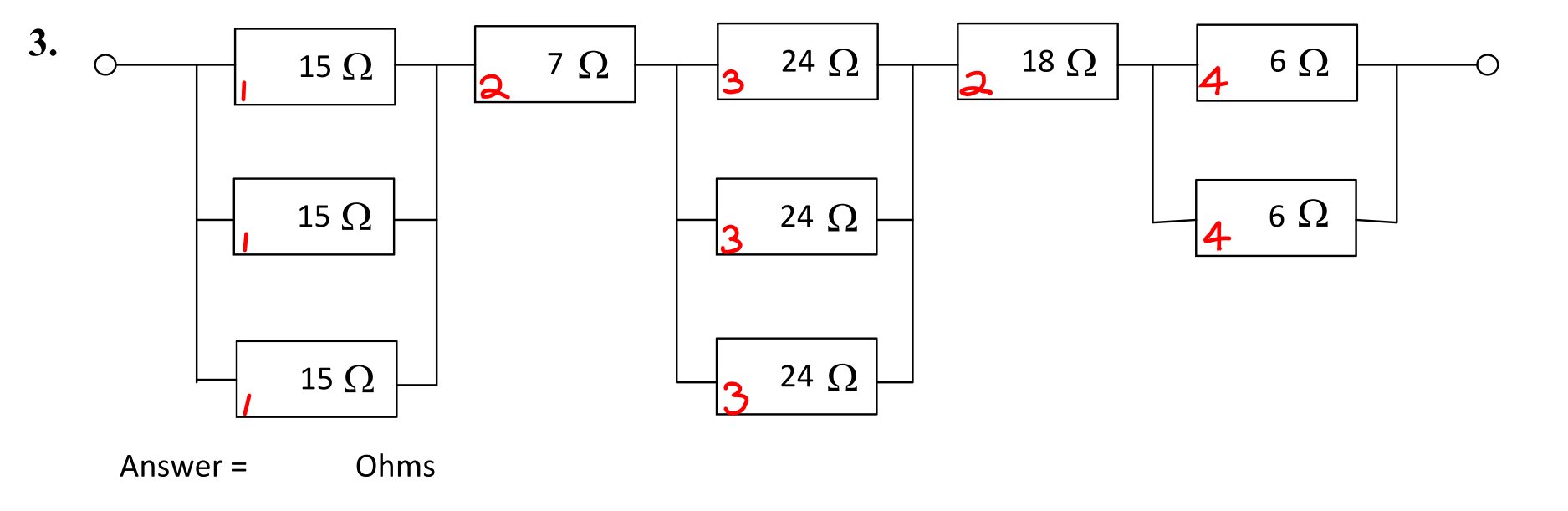
The resistors are grouped as shown.
Solution
The grouped resistances are calculated.
- \( R_1 = 15 \parallel 15 \parallel 15 = \frac{15}{3} \) = 5 Ω.
- \( R_2 = 7 + 18 \) = 25 Ω.
- \( R_2 = 24 \parallel 24 \parallel 24 = \frac{15}{3} \) = 8 Ω.
- \( R_2 = 6 \parallel 6 = \frac{15}{3} \) = 3 Ω.
The new equivalent circuit is shown below.

The total resistance \( R_{\mathrm{T}} \) can be calculated below.
\( R_{\mathrm{T}} = 5 + 25 + 8 + 3 \) = 41 Ω #.
Question 4
The circuit is shown below.

The groupings are as shown. There are a total of five initial groups.
Solution
We need to solve for \( R_1 \) through \( R_5 \).
- \( R_1 \) = 6 Ω.
- \( R_2 = 14 + 7 + 24 + 18 \) = 63 Ω.
- \( R_3 = 14 + 19 \) = 63 Ω.
- \( R_4 = 7 + 24 \) = 31 Ω.
- \( R_5 = R_4 \) = 31 Ω.
The new equivalent circuit is shown below.

The series-parallel network of \( R_3 \) through \( R_5 \) will be combined into a new resistance \( R_7 \).
\( R_7 = R_3 + R_4 \parallel R_5 = 33 + 31 \parallel 31 = 33 + \frac{31}{2} =33 + 15.5 \) = 48.5 Ω.
The simplified circuit is shown below.

The total resistance may now be calculated by direct inspection.
\( R_{\mathrm{T}} = R_1 + R_2 \parallel R_7 = 6 + 48.5 \parallel 63 = 6 + 27.4 \) = 33.4 Ω (3 sf) #.
The parallel resistance of \( R_2 \) and \( R_7 \) (27.4 Ω) has been treated numerically, as the actual expression \( \frac{6111}{223} \) is considered too unwieldy, and is unlikely to be simplified further through any more calculations.
Question 5
The circuit is shown below.

The groupings are as shown.
Solution
We need to solve for \( R_1 \) through \( R_4 \).
- \( R_1 = 17 + 25 + 19 \) = 61 Ω.
- \( R_2 = 3 + 2 + 5 \) = 10 Ω.
- \( R_3 = 45 \parallel 36 \) = 20 Ω.
- \( R_4 \) = 90 Ω.
The new equivalent circuit is shown below.
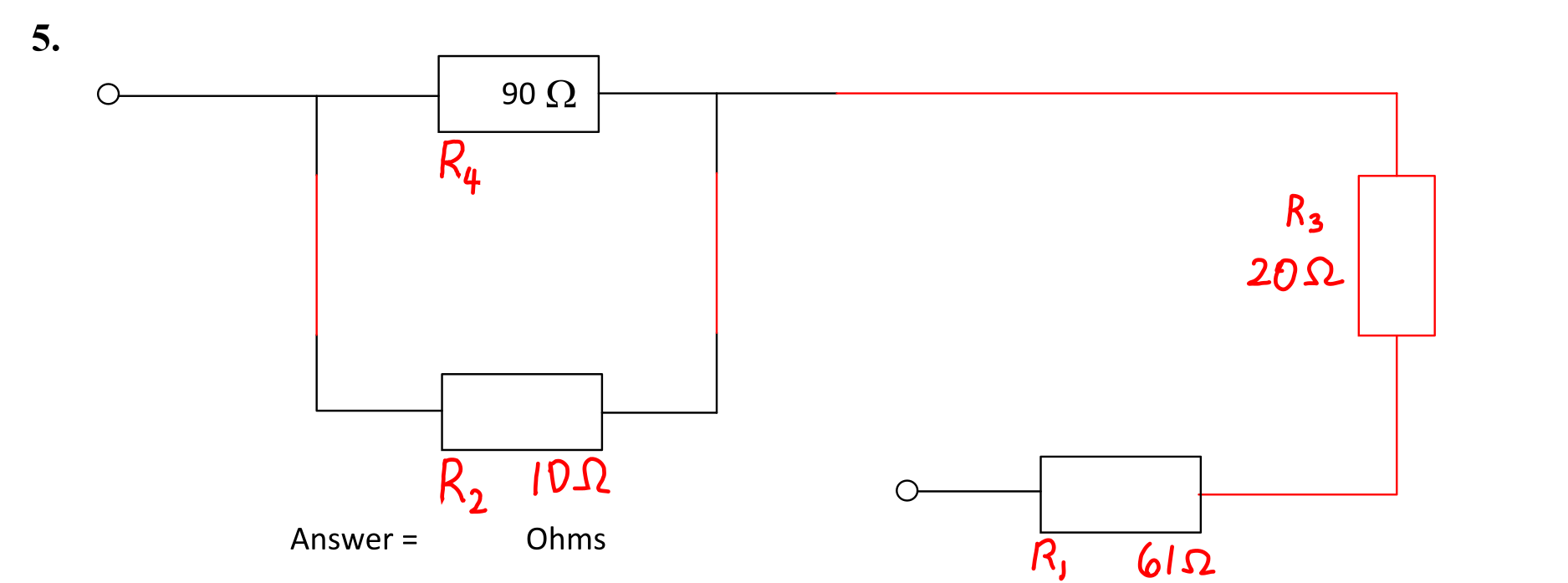
The circuit is now a simple series-parallel type, so we can calculate \( R_{\mathrm{T}} \) by direct inspection.
\( R_{\mathrm{T}} = R_1 + R_3 + R_2 \parallel R_4 = 81 + 90 \parallel 10 = 81 + 9 \) = 90 Ω #.