Book C: Area and Volume homework worksheet - Solutions and Commentary
Question 1
Calculate the area of a circle with radius 200 mm.
Solution
The formula for a the area of a circle is
\( A = \pi r^2 \)
where \( A \) is the area, and \( r \) is the radius of the circle.
In our case, \( r \) = 20 mm.
\( A = \pi r^2 = \pi \cdot 20^2 = \pi \cdot 400 \) = 1257 mm2 (4 sf).
NOTE: The radius was given in mm, so the calculated area is in mm2.
Question 2
Calculate the volume of a hot water cylinder with a 200 mm circular top, and a height of 1.5 m. Give the answer in both m3 and mm3.
Solution - Method 1 - Using Cylinder Diameter
The formula for a the volume of a cylinder is
\( V = \frac{\pi d^2 h}{4} \)
where \( V \) is the volume, \( d \) is diameter of the cylinder, and \( h \) is the height of the cylinder.
In our case, \( d \) = 200 mm, and \( h \) = 1.5 m.
In order to use this formula and get a clear result, it is essential that the height and diameter are both in the same units.
In this case, it appears easiest to convert the diameter to metres i.e. 200 mm → 0.2 m.
After converting all the domensions to the same units, the calculation can proceed.
\( V = \frac{\pi d^2 h}{4} = \frac{\pi \cdot 0.2^2 \cdot 1.5}{4} = \frac{0.1885}{4} = 0.04712\) m3 (4 sf) #.
NOTE: All the dimensions in the volume formula are in metres (m), so the volume will be in cubic metres (m3).
Converting to mm3 is easy: there are 109mm3 in 1 m3.
0.04712 m3 = 0.4712 · 109mm3 = 47120000 mm3 #.
Solution - Method 2 - Using Cylinder Radius
The formula for a the volume of a cylinder is
\( V = \pi r^2 h \)
where \( V \) is the volume, \( r \) is radius of the cylinder, and \( h \) is the height of the cylinder.
In our case, \( d \) = 200 mm, and \( h \) = 1.5 m. The radius of a circle is half the diameter, so \( r \) = 100 mm.
In order to use this formula and get a clear result, it is essential that the height and diameter are both in the same units.
In this case, it appears easiest to convert the radius to metres i.e. 100 mm → 0.1 m.
After converting all the domensions to the same units, the calculation can proceed.
\( V = \pi r^2 h = \pi \cdot 0.1^2 \cdot = 0.04712\) m3 (4 sf) #.
NOTE: All the dimensions in the volume formula are in metres (m), so the volume will be in cubic metres (m3).
Converting to mm3 is easy: there are 109 mm3 in 1 m3.
0.04712 m3 = 0.4712 · 109mm3 = 47120000 mm3 #.
Solution - Method 3 - Using millimetre dimensions
The formula for a the volume of a cylinder is
\( V = \frac{\pi d^2 h}{4} \)
where \( V \) is the volume, \( d \) is diameter of the cylinder, and \( h \) is the height of the cylinder.
In our case, \( d \) = 200 mm, and \( h \) = 1.5 m.
In order to use this formula and get a clear result, it is essential that the height and diameter are both in the same units.
In this case, the length can be converted to millimetres i.e. 1.5 m → 1500 mm.
After converting all the domensions to the same units, the calculation can proceed.
\( V = \frac{\pi d^2 h}{4} = \frac{\pi \cdot 200^2 \cdot 1500}{4} = \frac{188495559.2}{4} = 47120000\) mm3 (4 sf) #.
NOTE: All the dimensions in the volume formula are in millimetres (mm), so the volume will be in cubic millimetres (mm3).
Converting to m3 is easy: there are 10-9 m3 in 1 mm3.
47120000 mm3 = 47120000 · 10-9m3 = 0.04712 m3 #.
Question 3
Find the area of this shape
NOTE: The shape has been marked up with three areas, \( A_1 \), \( A_2 \), and \( A_3 \).
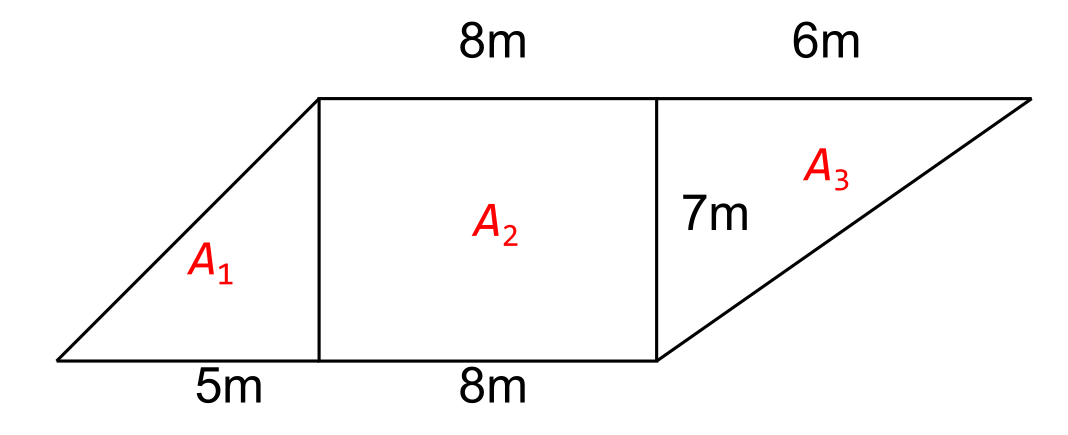
The area consists of two triangles (\(A_1\) and \(A_3\)), and one rectangle (\(A_2\)). The bases and heights of the triangles are known, and the side lengths of the dimensions are known.
The formula for the area of a triangle is
\(A = \frac{1}{2}bh\)
where \( A \) is the area of the triangle, \( b \) is the base length of the triangle, and \( h \) is the height of the triangle. It does not matter where the height is shown on the triangle, as long as the height is measured at right angles to the base. With that in mind, the base and height are actually interchangeable in the formula.
The formula for the area of a rectangle (or parallelogram) is
\( A = bh \)
where \( A \) is the area of the rectangle, \( b \) is the base length of the rectangle, and \( h \) is the height of the rectangle. It does not matter where the height is shown on the rectangle, as long as the height is measured at right angles to the base. With that in mind, the base and height are actually interchangeable in the formula.
The table below shows the calculations. For convenience, the bases will be considered the horizontal dimensions, and the heights vertical dimensions.
| Area | Shape | Area Formula |
\( b \) |
\( h \) |
Area |
|---|---|---|---|---|---|
| \( A_1 \) |
Triangle | \( \frac{1}{2} b h \) |
5 m |
7 m |
17.5 m2 |
| \( A_2 \) | Rectangle | \( b h \) | 8 m |
7 m |
56.0 m2 |
| \( A_3 \) | Triangle | \( \frac{1}{2} b h \) | 6 m |
7 m |
21.0 m2 |
| TOTAL | 94.5 m2 |
So the total area is 94.5 m2 #.
Question 4
How much volume of air is in this roof space?
NOTE: The shape has been marked up with the area, \( A \).

Solution
The roof space is a shape known as a triangular prism.
The formula for the volume of any prism is
\( V = A L \)
where \( V \) is the volume, \( A \) is the end face area of the prism, and \( L \) is the length of the prism.
In our case, we have a triangular prism, so the area formula is \( A = \frac{1}{2}bh \), where \( A \) is the area of the triangle, \( b \) is the base length of the triangle, and \( h \) is the height of the triangle.
With this in mind, the formula for the volume of a triangular prism is
\( V = \frac{1}{2} bhL \).
In this situation, \( b \) = 18 m, \( h \) = 8 m, and \( L \) = 25 m. All of the units have the same dimensions, so changing them is not required before using the formula.
Plugging these numbers into the volume formula gives us
\( V = \frac{1}{2} bhL = \frac{1}{2} \cdot 18 \cdot 8 \cdot 25 = \frac{1}{2} \cdot 3600 = \) 1800 m3 #.
Question 5
A 100m copper cable has 4 cores measuring 8mm diameter. When the copper is melted down and poured into a 500mm diameter container, how high will it be filled?
Solution - Method 1 - Volume Approach
This question is about determining volumes, and converting the volume to the filling height of a cylinder.
The first step is to determine the volume of the copper contained in the original cable.
The formula for the volume of a cylinder is
\( V = \frac{\pi d^2 L}{4} \)
where \( V \) is the volume, \( d \) is diameter of the cylinder, and \( L \) is the length of the cylinder. This formula is actually the same as the \( V = \frac{\pi d^2 h}{4} \) formula used in Question 2, except the term length is used instead of height.
The copper cable is 100 m long, and has four 8 mm diameter cores. This is the same as saying that the cable has 400 m length of a single 8 mm diameter core.
With this information, the volume of copper in the cable can be calculated. Note that we will have to get the length and diameter into the same unit. In this case, I will choose mm as the unit to work with. So the 400 m will be converted to 400000 mm.
The volume of copper in the cable is
\( V = \frac{\pi \cdot 8^2 \cdot 400000}{4} = \frac{80424771.93}{4} = \) = 20106200 mm3 (6 sf).
The next step is to find the fill height of the 500 mm diameter container.
We already know the formula for the volume of a cylinder, but we need to re-arrange the formula so that we can get the height.
\( V = \frac{\pi d^2 L}{4} \rightarrow 4 V = \pi d^2 L \rightarrow L = \frac{4 V}{\pi d^2} \)
We can now compute the fill height \( L \). For the 500 mm cylinder, \( V \) = 20106200 mm3, and \( d \) = 500 mm.
\(L = \frac{4 V}{\pi d^2} = \frac{4 \cdot 20106200}{\pi 500^2} = \frac{80424800}{785398} \) = 102.4 mm (4 sf).
The desired answer is in m, so the 102.4 mm is converted to 0.1024 m (4 sf) #.
Solution - Method 2 - Scaling approach
The formula for the volume of a cylinder is
\( V = \frac{\pi d^2 L}{4} \)
where \( V \) is the volume, \( d \) is diameter of the cylinder, and \( L \) is the length of the cylinder. This formula is actually the same as the \( V = \frac{\pi d^2 h}{4} \) formula used in Question 2, except the term length is used instead of height.
Rather than calculating the volume directly, we can use this formula to determine a scaling factor for the diameter, and use this factor to compute the new diameter directly from the previous one.
The copper cable is 100 m long, and has four 8 mm diameter cores. This is the same as saying that the cable has 400 m length of a single 8 mm diameter core.
The cylinder is 500 mm in diameter, and the copper fills the cylinder so that it has the same volume of copper as in the original cable. In other words, \( V \) is constant.
\( \frac{V_2}{V_1} = \frac{\pi d_2^2 L_2}{4} \cdot \frac{4}{\pi d_1^2 L_1} = \frac{d_2^2 L_2}{d_1^2 L_1} \)
Since the volume is constant, \( \frac{V_2}{V_1} = 1 \), so the formula becomes
\( \frac{d_2^2 L_2}{d_1^2 L_1} = 1\).
We can solve this formula for \( L_2 \), which we will use to represent the "height" of the cylinder.
\( L_2 = L_1 \cdot \left(\frac{d_1}{d_2} \right)^2\).
We have the formula we need. In our case, \( L_1 \) = 400 m, \( d_1 \) = 8 mm, \( d_2 \) = 500 mm. Plugging these figures in gives us the answer.
\( L_2 = 400 \cdot \left(\frac{8}{500} \right)^2 = 400 \cdot \left(\frac{4}{125} \right)^2 = 400 \cdot 0.000256 \) = 0.1024 m #.
Notice two things about this method:
- It was not necessary to actually calculate any volumes.
- It did not matter what units \( d_1 \) and \( d_2 \) were in, as long as they were the same units. The units cancel out because they are used in a ratio.