Book C: Pythagoras worksheet 1 - Solutions and Commentary

Introduction

Pythagoras' Theorem applies to right angled triangles. A right angled triangle has two sides \( a \) and \( b \), and a hypotenuse \( c \) that is always opposite the right angle. With that defined, we can use some formulas.

The picture below demonstrates the formula. The area of the attached square 'c' is the sum of the areas of the squares 'a' and 'b'.

The general form of the Pythagoras Theorem is the following:

\( c^2 = a^2 + b^2 \)

where \( c \) is the length of the hypotenuse, and \( a \) and \( b \) are the lengths of the other two sides.

NOTE: There is no particular "order" for \( a \) and \( b \). They are just the two sides that are not the hypotenuse.

The formula above is an implicit formula, meaning that \( c \) is defined implicitly as \( c^2 \).

Solving for the hypotenuse (\( c \))

The formula for \( c \) is as follows.

\( c = \sqrt{a^2 + b^2} \)

Normally, the square root precedes the \( a^2 + b^2 \). However, it is also possible to do the same thing using powers. Taking the square root if a number is the same as raising the number to the power of 0.5.

\( c = \left(a^2 + b^2\right)^{0.5} \)

This form may be easier to do on your calculator.

Solving for \( a \) and \( b \)

The formulas for \( a \) and \( b \) are obtained by rearranging the formula for \( c^2 \).

\( c^2 = a^2 + b^2 \rightarrow a^2 = c^2 - b^2 \)

The formula is similar for \( b^2 \): \( b^2 = c^2 - a^2 \)

The explicit formulas for \( a \) and \( b \) are as follows:

• \( a = \sqrt{c^2 - b^2} \)
• \( b = \sqrt{c^2 - a^2} \)

Question 1

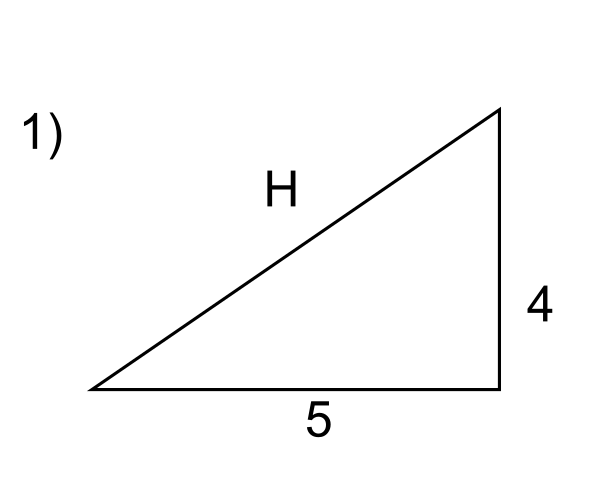
The side H is opposite the right angle, so it is the hypotenuse.

The other side lengths \( a \) and \( b \) are 4 and 5 respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{4^2 + 5^2} = \sqrt{41} \) = 6.40 (2 dp) #.

Question 2

In this case the sides appear to be given dimensions of metres, this is ok as long as all sides have the same dimensions when put into the formulas.

The side j is opposite the right angle, so it is the hypotenuse.

The other side lengths \( a \) and \( b \) are 4 m and 6 m respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{4^2 + 6^2} = \sqrt{52} \) = 7.21 m (2 dp) #.

Since the side lengths are given in m, the hypotenuse will also be in m.

Question 3

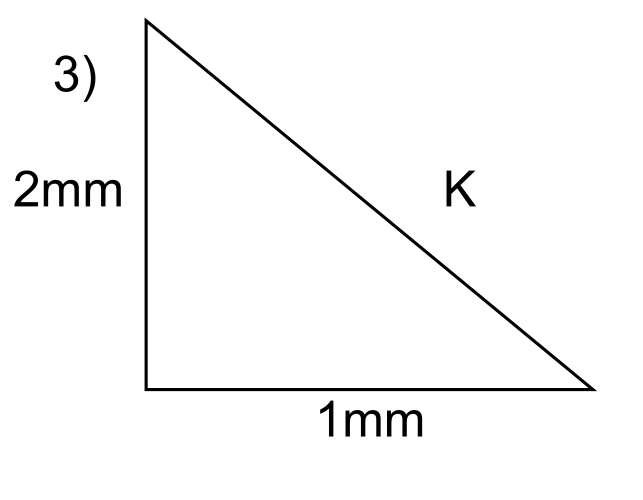
In this case the sides appear to be given dimensions of millimetres, this is ok as long as all sides have the same dimensions when put into the formulas.

The side j is opposite the right angle, so it is the hypotenuse.

The other side lengths \( a \) and \( b \) are 1 mm and 2 mm respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{1^2 + 2^2} = \sqrt{5} \) = 2.24 mm (2 dp) #.

Since the side lengths are given in mm, the hypotenuse will also be in mm.

Question 4

The side V is opposite the right angle, so it is the hypotenuse. It does not matter what the orientation of the triangle is, the hypotenuse is always opposite the right angle.

The other side lengths \( a \) and \( b \) are 4 and 8 respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{4^2 + 8^2} = \sqrt{80} \) = 8.94 (2 dp) #.

Question 5

In this case the sides appear to be given dimensions of millimetres, this is ok as long as all sides have the same dimensions when put into the formulas.

The side m is opposite the right angle, so it is the hypotenuse. It does not matter what the orientation of the triangle is, the hypotenuse is always opposite the right angle.

The other side lengths \( a \) and \( b \) are 7 mm and 11 mm respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{7^2 + 11^2} = \sqrt{170} \) = 13.04 mm (2 dp) #.

Since the side lengths are given in mm, the hypotenuse will also be in mm.

Question 6

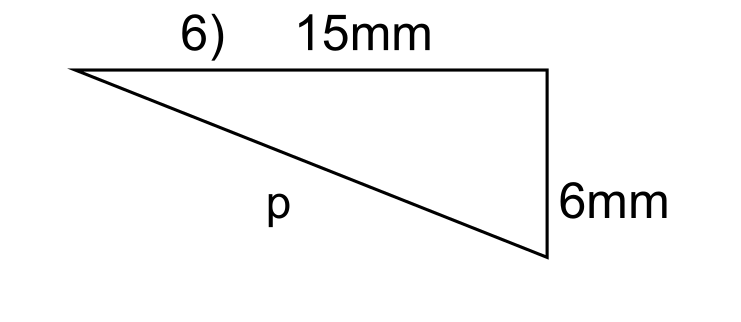
In this case the sides appear to be given dimensions of millimetres, this is ok as long as all sides have the same dimensions when put into the formulas.

The side p is opposite the right angle, so it is the hypotenuse.

The other side lengths \( a \) and \( b \) are 6 mm and 15 mm respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{6^2 + 15^2} = \sqrt{261} \) = 16.16 mm (2 dp) #.

Since the side lengths are given in mm, the hypotenuse will also be in mm.

Question 7

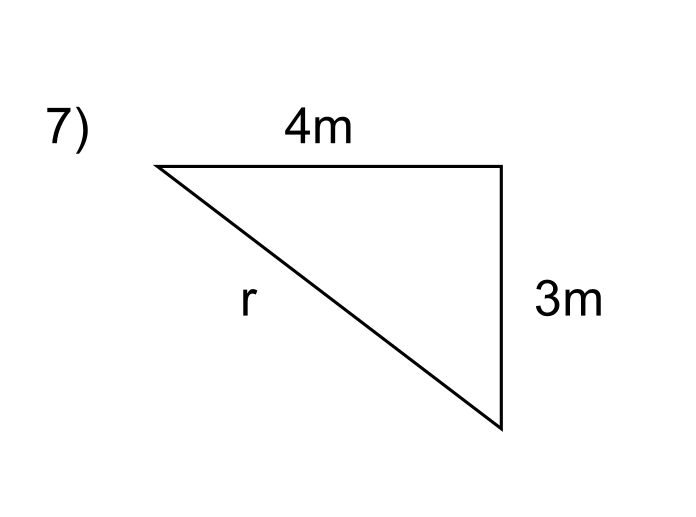
In this case the sides appear to be given dimensions of metres, this is ok as long as all sides have the same dimensions when put into the formulas.

The side r is opposite the right angle, so it is the hypotenuse.

The other side lengths \( a \) and \( b \) are 3 m and 4 m respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{25} \) = 5 m #.

This type of right-angled triangle, with all integer sides, is known as a Pythagorean Triple. There are infinitely many of them, but (3, 4, 5) is the only one that has three consecutive integers as side lengths.

Question 8

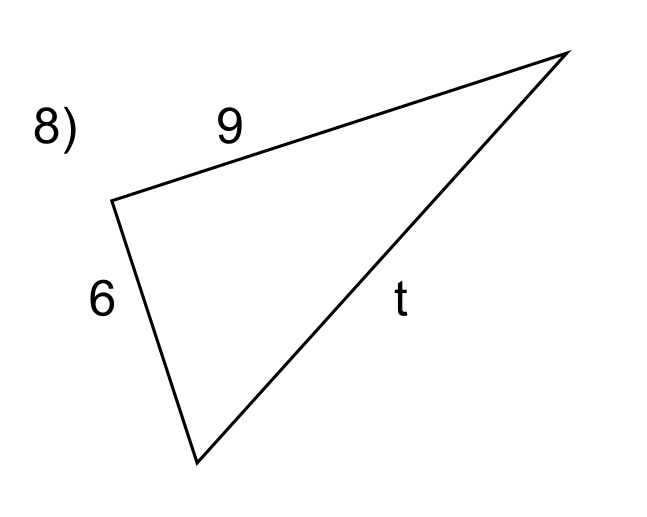
The side t is opposite the right angle, so it is the hypotenuse. It does not matter what the orientation of the triangle is, the hypotenuse is always opposite the right angle.

The other side lengths \( a \) and \( b \) are 6 and 9 respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{6^2 + 9^2} = \sqrt{117} \) = 10.82 (2 dp) #.

Question 9

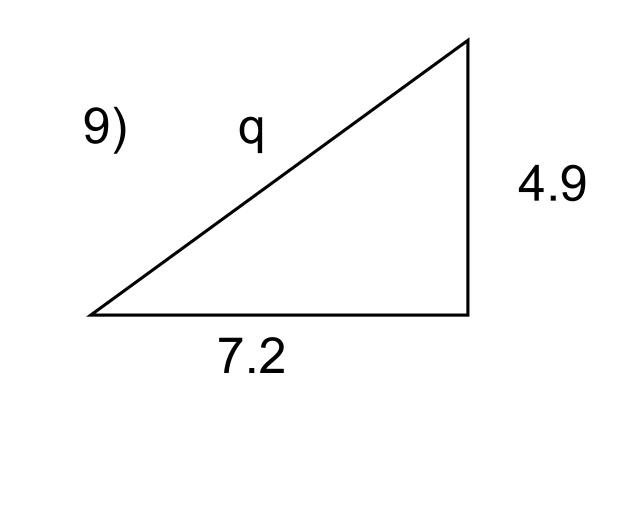
The side t is opposite the right angle, so it is the hypotenuse.

The other side lengths \( a \) and \( b \) are 4.9 and 7.2 respectively.

The hypotenuse is solved using the explicit formula above.

\( c = \sqrt{a^2 + b^2} = \sqrt{4.9^2 + 7.2^2} = \sqrt{75.85} \) = 8.71 (2 dp) #.