Introduction

These circuits are worked out using series-parallel circuit calculations. The maximum simplification is that there are no nested parallel circuits at each step.

In other words:

  • Calculations like \( R_1 + (R_2 + R_3) \parallel (R_4 + R_5) \parallel (R_6 + R_7) \) are done in a single step.
  • Calculations like \( R_1 + (R_2 + R_3) \parallel (R_4 + R_5 \parallel (R_6 + R_7)) \) are broken down into multiple steps, due to the nested parallel calculation.

These rules are followed throughout these solutions.


Question 1

The circuit is shown below, with the resistors grouped into simple series-parallel sections.


Solution

The first step is to calculate the resistances as shown.

  • \( R_1 = \) 25 Ω.
  • \( R_2 = (10 + 8 + 3) + 21 \parallel 28 = 21 + 12 = \) 33 Ω.
  • \( R_3 = 28 + 28 = \) 56 Ω.
  • \( R_4 = \) 30 Ω.
  • \( R_5 = (12 + 18) + 30 \parallel 70 = 30 + 21 = \) 51 Ω.

The circuit with these resistances calculated is shown below.


There is a new resistance, \( R_6 \), that requires calculation. The relevant resistances are shown below.

  • \( R_1 = \) 25 Ω.
  • \( R_2 = \) 33 Ω.
  • \( R_6 = R_3 + R_4 \parallel R_5 = 56 + 30 \parallel 51 = 56 + \frac{170}{9} = \frac{674}{9} = \) 74.8889 Ω (6 sf).

The circuit with these resistances calculated is shown below.


The total resistance, \( R_{\mathrm{T}} \), can now be calculated. The relevant resistances and calculations are shown below.

  • \( R_1 = \) 25 Ω.
  • \( R_2 = \) 33 Ω.
  • \( R_{\mathrm{T}} = R_1 + R_2 \parallel R_6 = 25 + 33 \parallel \frac{674}{9} = 25 + \frac{22242}{971} = 25 + 22.9063 = \) 47.91 Ω (4 sf).

The final version of this circuit is shown below.



Question 2

The circuit is shown below, with the resistors grouped into simple series-parallel sections.


Solution

The first step is to calculate the resistances as shown.

  • \( R_1 = \) 21 Ω.
  • \( R_2 = 28 + 28 = \) 56 Ω.
  • \( R_3 = \) 35 Ω.
  • \( R_4 = 28 \parallel 28 \parallel (4 + 28 + 3) = 14 \parallel 35 = \) 10 Ω.

The circuit with these resistances calculated is shown below.


There is a new resistance, \( R_5 \), that requires calculation. The relevant resistances are shown below.

  • \( R_1 = \) 21 Ω.
  • \( R_2 = \) 56 Ω.
  • \( R_5 = R_2 \parallel (R_3 + R_4) = 56 \parallel (35 + 10) = 56 \parallel 45 = \frac{2520}{101} = \) 24.9505 Ω (6 sf).

The circuit with these resistances calculated is shown below.


The total resistance, \( R_{\mathrm{T}} \), can now be calculated. The relevant resistances and calculations are shown below.

  • \( R_1 = \) 21 Ω.
  • \( R_5 = \) 24.9505 Ω.
  • \( R_{\mathrm{T}} = R_1 + R_5 = 21 + 24.9505 = \) 45.95 Ω (4 sf).

The final version of this circuit is shown below.



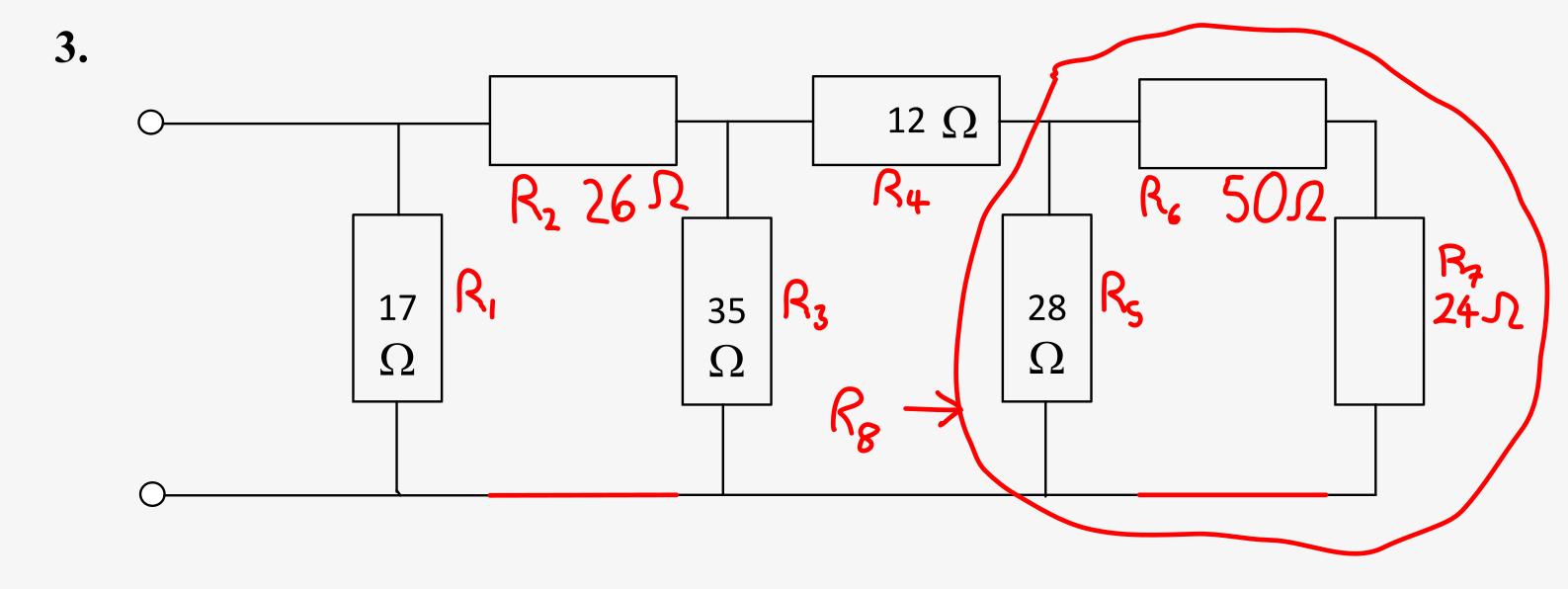
Question 3

The circuit is shown below, with the resistors grouped into simple series-parallel sections.


NOTE: It is possible to create the groupings of \( R_2 \) and \( R_6 \) as shown because these resistors would have the same current flowing through them in-circuit. Any resistors in this situation are in series.

Solution

The first step is to calculate the resistances as shown.

  • \( R_1 = \) 17 Ω.
  • \( R_2 = 19 + 7 = \) 26 Ω.
  • \( R_3 = \) 35 Ω.
  • \( R_4 = \) 12 Ω.
  • \( R_5 = \) 28 Ω.
  • \( R_6 = 20 + 30 = \) 50 Ω.
  • \( R_7 = 33 \parallel (15 + 45 + 28) = 33 \parallel 88 = \) 24 Ω.

The circuit with these resistances calculated is shown below.


There is a new resistance, \( R_8 \), that requires calculation. The relevant resistances are shown below.

  • \( R_1 = \) 17 Ω.
  • \( R_2 = \) 26 Ω.
  • \( R_3 = \) 35 Ω.
  • \( R_4 = \) 12 Ω.
  • \( R_5 = \) 28 Ω.
  • \( R_6 = \) 50 Ω.
  • \( R_7 = \) 24 Ω.
  • \( R_8 = R_5 \parallel (R_6 + R_7) = 28 \parallel (50 + 24) = 28 \parallel 74 = \frac{1036}{51} = \) 20.3137 Ω (6 sf).

The circuit with these resistances calculated is shown below.


There is a new resistance, \( R_9 \), that requires calculation. The relevant resistances are shown below.

  • \( R_1 = \) 17 Ω.
  • \( R_2 = \) 26 Ω.
  • \( R_3 = \) 35 Ω.
  • \( R_4 = \) 12 Ω.
  • \( R_8 = \frac{1036}{51} = \) 20.3137 Ω (6 sf).
  • \( R_9 = R_3 \parallel (R_4 + R_8) = 35 \parallel (12 + \frac{1036}{51}) = 35 \parallel 32.3137 = \) 16.8016 Ω (6 sf). There's not much point trying to preserve the fractions from now on, as they become unmanageable. All resistances will be handled numerically.

The circuit with these resistances calculated is shown below.


The total resistance, \( R_{\mathrm{T}} \), can now be calculated. The relevant resistances and calculations are shown below.

  • \( R_1 = \) 17 Ω.
  • \( R_2 = \) 26 Ω.
  • \( R_9 = \) 16.8016 Ω.
  • \( R_{\mathrm{T}} = R_1 \parallel (R_2 + R_9) = 17 \parallel (26 + 16.8016) = 17 \parallel 42.8016 = \) 12.17 Ω (4 sf).

The final version of this circuit is shown below.


Last modified: Thursday, 14 May 2020, 11:48 AM