Book "B": Worksheet 6: Efficiency and Horsepower Assignment - Answers and Commentary
Question 1
This question involves filling in a table. The answers are shown in bold.
| Input | Output | Comment |
|---|---|---|
| 10 hp |
7.46 kW |
1 hp = 0.746 kW |
| 0.5 hp |
373 W |
1 hp = 746 W |
| 1 kW |
1.340 hp | 1 kW = 1.340 hp |
| 5 MJ |
1.389 unit | 1 MJ = 0.2778 unit |
| 500 W for 10 hours |
18 MJ | 1 Wh = 3600 J |
| 45 W |
0.06032 hp |
1 W = 0.00134048 hp |
Question 2
This question involves completing the missing words in a text passage. The answers are shown in bold.
Input power = Output power plus losses. Efficiency is the ratio of useful power output to total power input. The symbol for efficiency is \( \eta \) and the unit is dimensionless. Efficiency is normally stated as a percentage.
Comments
This sentence is a correct summary of what efficiency means, and how to compute it. The symbol \( \eta \) is the Greek small letter eta. Efficiency can be stated as a percentage, but can also be given as a ratio.
The efficiency is always less than one.
Question 3
A motor has losses of 500 W and an output power rating of 2 hp. Calculate the input power.

Solution
Before proceeding, we need to make sure we are "comparing apples with apples". The power units need to be consistent with each other to make the input power calculation meaningful.
It is easier to work with watts, as doing so avoids dividing by 746.
The motor's output power (\( P_{\mathrm{out}} \)) is 2 hp, or 1492 W.
The losses (\( P_{\mathrm{loss}} \)) are 500 W.
The input power (\( P_{\mathrm{in}} \)) is 1992 W #.
Question 4
What is the efficiency of a motor if the input power is 2300 W and the output power is 2000 W?
Solution
The power units are consistent with each other, so making the efficiency calculation straightforward.
The motor's output power (\( P_{\mathrm{out}} \)) is 2000 W.
The input power (\( P_{\mathrm{in}} \)) is 2300 W.
The efficiency is calculated as shown below.
\( \eta = \frac{P_{\mathrm{out}}}{P_{\mathrm{in}}} = \frac{2000}{2300} = \) 0.897 or 89.7%.
Question 5
A motor draws 15 amps from a 200 volt supply. If the motor is 60% efficient calculate the output power in horsepower?
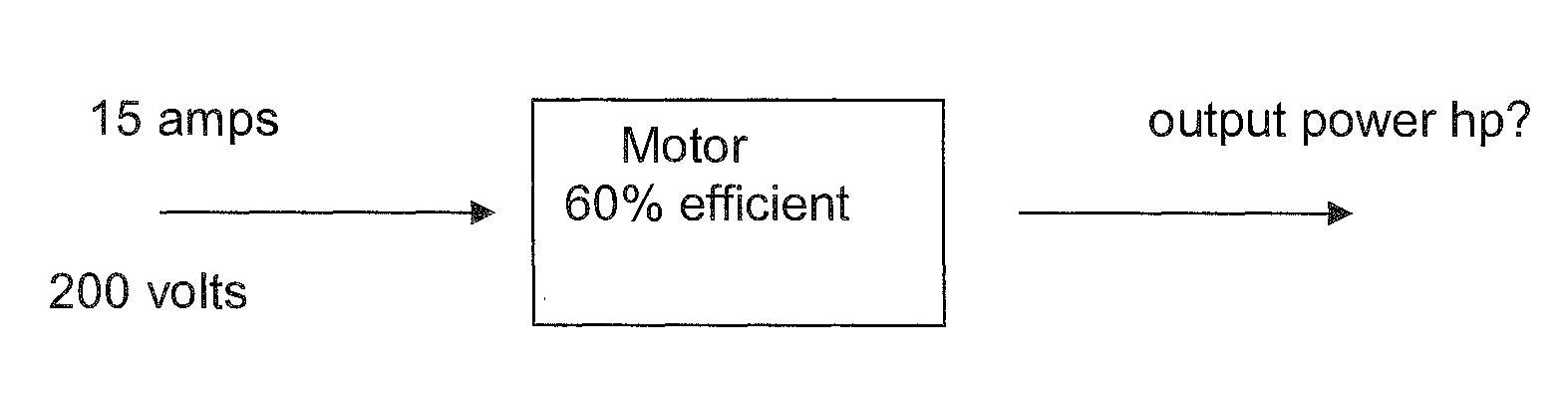
Solution
The motor's input power (\( P_{\mathrm{out}} \)) is \( 200 \cdot 15 = \) 3000 W.
The efficiency (\(\eta)\) is 60%, or 0.6.
The output power is calculated below.
\( P_{\mathrm{out}} = \eta P_{\mathrm{in}} = 0.6 \cdot 3000 = \) 1800 W.
The question wants the answer in horsepower (hp). \( P_{\mathrm{out}} = \frac{1800}{746} = \) 2.41 hp #.
Question 6
An ac motor is driving a dc generator.
The motor draws 36 amps from a 230 volt supply.
The motor has an efficiency of 85% while the generator runs at 75% efficiency.
The generator has an output voltage of 115 volts.
Sketch a block diagram showing the above information in the format illustrated in question 5.
Add to the diagram:
- motor input power;
- motor output power;
- generator output power;
- generator output current.
and calculate each of these four values.
Solution
This question concerns energy that goes through a chain of transformations. The chain is shown below.

The efficiency of the total system, \( \eta_{\mathrm{tot}} \), is the product of the efficiencies of each system in the chain.
\( \eta_{\mathrm{tot}} = \eta_1 \eta_2 \ldots \eta_n \)
For this system, the total efficiency is calculated below.
\( \eta_{\mathrm{tot}} = \eta_1 \eta_2 = 0.85 \cdot 0.75 = \) 0.6375 or 63.8%.
The input power \( P_{\mathrm{m,in}} \) is the power supplied to the motor.
\( P_{\mathrm{m,in}} = V I = 230 \cdot 36 = \) 8280 W #.
The motor output power is calculated below.
\( P_{\mathrm{m,out}} = \eta_{\mathrm{m}} P_{\mathrm{m,in}} = 0.85 \cdot 8280 = \) 7038 W #.
The total output power is calculated below, using the input power and the efficiency.
\( P_{\mathrm{g,out}} = \eta_{\mathrm{tot}} P_{\mathrm{m,in}} = 0.6375 \cdot 8280 = \) 5279 W #.
The motor has an output voltage of 115 V, and an output power of 5279 W. The current is calculated below.
\( I = \frac{P}{V} = \frac{5279}{115} = \) 45.90 A #.
Question 7
A motor draws 2.3 amps from a 230 volts mains.
The motor is 65% efficient and this motor drives a gearbox that is 90% efficient.
Draw a block diagram showing inputs and outputs and calculate the gearbox output power in hp.
Solution - Method 1 - Direct Calculation
The output power may be calculated directly from the input power and the "chained" efficiency of the system as a whole.
A drawing of the whole system showing the power flow is shown below.

The motor (and system) input power \( P_{\mathrm{in}} \) is \( 230 \cdot 2.3 \) = 529 W.
The efficiency of the system as a whole is the product of the efficiencies of all the sub-systems.
The motor efficiency \( \eta_1 \) is 0.65.
The gearbox efficiency \( \eta_2 \) is 0.90.
The total efficiency \( \eta \) is \( 0.65 \cdot 0.90 \) = 0.585, or 58.5%.
The output power \( P_{\mathrm{out}} \) is \( P_{\mathrm{out}} = \eta P_{\mathrm{in}} = 0.585 \cdot 529 = \) 309.465 W (6 sf).
The final answer is wanted in horsepower. Given that 1 hp = 746 W, \( P_{\mathrm{out}} = \frac{309.465}{746} = \) 0.4148 hp (4 sf) #.
Solution - Method 2 - Stage-by-Stage Method
This method calculates the output power at every stage. The output power at one stage is used for the input power to the next stage.
A drawing of the whole system showing the power flow is shown below.

A table of the calculations is shown below.
The SYSTEM row is calculated in the following way:
- The input power value is the maximum input power value.
- The output power value is the minimum input power value.
- The efficiency value is the product of all the efficiencies.
The output power of the gearbox is shown in bold.
| Component | Input Power | Efficiency | Output Power | Comment |
|---|---|---|---|---|
| Motor |
529 W | 0.65 | 343.85 W | |
| Gearbox |
343.85 W | 0.90 | 309.465 W | The motor output power is the gearbox input power. |
| SYSTEM | 529 W | 0.585 | 309.465 W |
The final answer is wanted in horsepower. Given that 1 hp = 746 W, \( P_{\mathrm{out}} = \frac{309.465}{746} = \) 0.4148 hp (4 sf) #.
Question 8
Calculate the input current to a motor that has an efficiency of 55% and an output of 1 hp.
The supply is 200 volts.
Create a labelled drawing and show all working.
NOTE: It is possible to create a labelled diagram, but since there is only one component, the diagram won't be particularly interesting.
Solution
The motor output power \( P_{\mathrm{out}} \) is 1 hp, or 746 W.
The motor efficiency \( \eta \) is 0.55.
The motor is the only component, so the total efficiency is also 0.55.
The input power is found from the equation \( P_{\mathrm{out}} = \eta P_{\mathrm{in}} \).
\( P_{\mathrm{out}} = \eta P_{\mathrm{in}} \rightarrow P_{\mathrm{in}} = \frac{P_{\mathrm{out}}}{\eta} \)
The output power and efficiency can be plugged into the input power formula.
\( P_{\mathrm{in}} = \frac{P_{\mathrm{out}}}{\eta} = \frac{746}{0.55} = \) 1356.36 W.
The current is now calculated.
\( I = \frac{P_{\mathrm{in}}}{V} = \frac{1356.36}{200} = \) 6.782 A (4 sf) #.
Question 9
A generator supplies a load consisting of 8 parallel lamps that are each 100W.
Find the generator's input power if the generator is 80% efficient.
Solution
The generator output power \( P_{\mathrm{out}} \) is \( 8 \cdot 100 \), or 800 W, since there are 8 100 W lamps.
The generator efficiency \( \eta \) is 0.80.
The generator is the only component, so the total efficiency is also 0.80.
The input power is found from the equation \( P_{\mathrm{out}} = \eta P_{\mathrm{in}} \).
\( P_{\mathrm{out}} = \eta P_{\mathrm{in}} \rightarrow P_{\mathrm{in}} = \frac{P_{\mathrm{out}}}{\eta} \)
The output power and efficiency can be plugged into the input power formula.
\( P_{\mathrm{in}} = \frac{P_{\mathrm{out}}}{\eta} = \frac{800}{0.8} = \) 1000 W #.