Worksheet 16C - Harder Series-Parallel calculations - Solutions and Commentary

Question 1

A marked-up version of the circuit is shown below.

The objective is to find the following quantities:

• The supply voltage \( V_{\mathrm{s}} \).
  
• The current through \( R_1 \): \( I_{R1} \).
  

The following quantities are known:

• The current through \( R_4 \) is 10 A i.e. \( I_{R4} = 10 A \).
  

Solution

\( R_4 \) has 10 A current flow through it. The combination of \( R_2 \) through \( R_4 \) has a total supply voltage across it. The supply voltage is calculated using Ohm's Law.

\( V_{\mathrm{s}} = I_{\mathrm{R3}} \cdot (R_2 + R_3 + R_4) = 10 \cdot (6 + 9 + 5 ) = 10 \cdot 20 = \) 200 V #.

The current through \( R_1 \) is calculated using the supply voltage and Ohm's Law.

\( I_{R1} = \frac{V_{\mathrm{s}}}{R_1} = \frac{200}{20} = \) 10 A #.

Question 2

A marked-up version of the circuit is shown below.

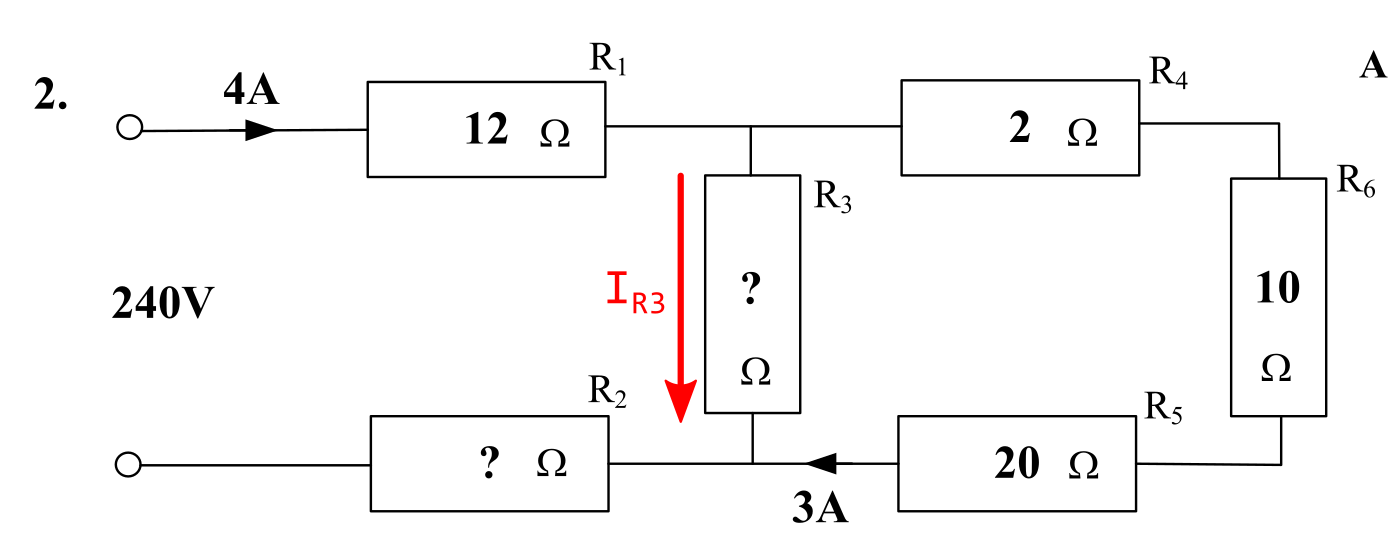
The objective is to find the following quantities (as listed):

• The current through \( R_3 \).
  
• The unknown resistance \( R_{3} \).
  
• The unknown resistance \( R_{2} \).
  

The following quantities are known:

• The current through \( R_4 \) through \( R_6 \) is 3 A.
  
• The supply voltage \( V_{\mathrm{s}} \) is 240 V.
  
• The supply current \( I_{\mathrm{s}} \) is 4 A.
  

Solution

The current through \( R_3 \) is 1 A, calculated using Kirchhoff's Current Law.

\( I_{R3} = 4 - 3 = \) 1 A #.

The voltage across \( R_3 \) is the same as the total voltage drop across the resistors \( R_4 \), \( R_5 \) and \( R_6 \).

\( V_{\mathrm{R3}} = 3 \cdot (2 + 20 + 10) = 3 \cdot 32 = \) 96 V.

\( R_3 \) is now calculated using Ohm's Law.

\( R_3 = \frac{V_{R3}}{I_{R3}} = \frac{96}{1} = \) 96 Ω #.

\( R_2 \) is calculated using Kirchhoff's Voltage Law and Ohm's Law.

\( V_{R2} = V_{\mathrm{s}} - V_{R1} - V_{R3} = 240 - 12 \cdot 4 - 96 = 240 - 48 - 96 = 240 - 144 = \) 96 V.

The resistance is calculated using Ohm's Law.

\( R_2 = \frac{V_{R2}}{I_{R2}} = \frac{96}{4} = \) 24 Ω #.

Question 3

A marked-up version of the circuit is shown below.

The objective is to find the following quantities:

• The resistance of resistor \( R_7 \).
  

The following quantities are known:

• The supply voltage \( V_{\mathrm{s}} \) is 100 V.
  
• The supply current \( I_{\mathrm{s}} \) is 4 A.
  

Solution

This circuit may be solved using repeated current splitting and voltage drop calculations.

The supply current is 4 A. Of this current, 1.25 A (\( \frac{100}{80} \)) will flow through \( R_1 \), leaving 2.75 A flowing through \( R_2 \) and \( R_3 \).

The voltage across \( R_4 \) can be calculated.

\( V_{R4} = V_{\mathrm{s}} - 2.75 \cdot (11.5 + 6) = 100 - 48.125 = \) 51.875 V (6 sf).

The current through \( R_5 \), \( R_6 \) and \( R_7 \) can be calculated.

\( I_{R5} = 2.75 - \frac{V_{R4}}{R_4} = 2.75 - \frac{51.875}{75} = 2.75 - 0.691667 = \) 2.05833 A (6 sf).

Given a current of 2.05833 A, and a voltage drop of 51.875 V, the voltage across \( R_7 \) is calculated.

V_{R7} = V_{R4} - V_{R5} - V_{R6} = 51.875 - 2.05833 \cdot (12 + 3.3) = 51.875 - 31.4925 = \) 20.3825 V (6 sf).

The resistance \( R_7 \) is now calculated using Ohm's Law.

\( R_7 = \frac{V_{R7}}{I_{R5}} = \frac{20.3825}{2.05833} = \) 9.902 Ω (4 sf) #.

Question 4

A marked-up version of the circuit is shown below.

The objective is to find the following quantities:

• The supply voltage \( V_{\mathrm{s}} \).
  
• The total load resistance \( R_{\mathrm{T}} \).
  
• The resistance of resistor \( R_9 \).
  

The following quantities are known:

• The voltage drop across resistor \( R_3 \) is 165 V.
  
• The current through \( R_4 \) is 3.5 A.
  
• The current through \( R_8 \) is 2 A.
  
• The voltage drop across resistor \( R_9 \) is 12 V.
  

Solution - Method 1 - "Minimal Calculations" Method

\( R_9 \) has a voltage drop of 12 V, and a current of 2 A.

\( R_9 = \frac{12}{2} = \) 6 Ω #.

The total resistance \( R_{\mathrm{T}} \) is now calculated.

The supply current \( I_{\mathrm{s}} \) is the sum of the 3.5 A through \( R_4 \) and the current flow through \( R_3 \).

\( I_{\mathrm{s}} = 3.5 + \frac{165}{33} = 3.5 + 5 = \) 8.5 A.

The supply voltage \( V_{\mathrm{s}} \) is calculated using the voltage drops across \( R_1 \), \( R_2 \) and \( R_3 \).

\( V_{\mathrm{s}} = I_{\mathrm{s}} \cdot (R_1 + R_2) + V_{R3} = 8.5 \cdot (16 + 10) + 165 = 221 + 165 = \) 386 V #.

The total load resistance \( R_{\mathrm{T}} \) is simply the ratio of the supply voltage to the supply current.

\( R_{\mathrm{T}} = \frac{V_{\mathrm{s}}}{I_{\mathrm{s}}} = \frac{386}{8.5} = \) 45.41 Ω (4 sf) #.

Not that it is not necessary to calculate the values of \( R_5 \) and \( R_6 \) to solve for the quantities required.

Solution - Method 2 - "Whole Circuit Solution" Method

The total resistance \( R_{\mathrm{T}} \) is calculated. This is done by "collapsing" the circuit from right to left.

\( R_9 \) has a voltage drop of 12 V, and a current of 2 A.

\( R_9 = \frac{12}{2} = \) 6 Ω #.

\( V_{R6} = V_{R9} + I_{R9} \cdot (R_7 + R_8) = 12 + 2 \cdot 32 = 12 + 64 = \) 76 V.

The current flow through \( R_6 \) is 1.5 A, due to the current split of 3.5 A and 2 A.

\( R_6 = \frac{V_{R6}}{I_{R6}} = \frac{76}{1.5} = \) 50.6667 Ω (6 sf).

The resistance as "seen" by \( R_4 \) and \( R_5 \) is the ratio of the 76 V voltage drop across \( R_6 \) to the 3.5 A total current. This resistance will be called \( R_{\mathrm{a}} \).

\( R_{\mathrm{a}} = \frac{76}{3.5} = \) 21.7143 Ω (6 sf).

This should also be the same as the total resistance of \( R_6 \) through \( R_9 \).

\( R_{\mathrm{a}} = 50.6667 \parallel (16 + 16 + 6) = 50.6667 \parallel 38 = \) 21.7143 Ω (6 sf).

The next step is to compute \( R_5 \).

The voltage drop across \( R_3 \) is 165 V. The voltage drop across R_6 is 76 V. The voltage drop across R_4 is \( 16 \cdot 3.5 = \) 52 V. The calculation of the voltage drop across R_5 is shown below.

\( V_{R5} = V_{R3} - V_{R4} - V_{R_6} = 165 - 3.5 \cdot 16 - 76 = 165 - 56 - 76 = \) 33 V.

The resistance is calculated using Ohm's Law.

\( R_5 = \frac{V_{R5}}{I_{R5}} = \frac{33}{3.5} = \) 9.42857 Ω (6 sf).

The resistance as "seen" by \( R_1 \) and \( R_2 \) is the ratio of the 165 V voltage drop across \( R_3 \) to the 8.5 A total current. This resistance will be called \( R_{\mathrm{b}} \).

\( R_{\mathrm{b}} = \frac{165}{8.5} = \) 19.4118 Ω (6 sf).

This should also be the same as the total resistance of \( R_3 \), \( R_4 \), \( R_5 \), and \( R_{\mathrm{a}} \).

\( R_{\mathrm{b}} = 33 \parallel (16 + 21.7143 + 9.42857) = 33 \parallel 47.1429 = \) 19.4118 Ω (6 sf).

The total resistance is the sum of the remaining resistances.

\( R_{\mathrm{T}} = R_1 + R_{\mathrm{b}} + R_2 = 16 + 19.4118 + 10 = \) 45.4118 Ω (6 sf) or 45.41 Ω (4 sf) #.

This method is significantly more complicated. In particular, it involved the "wasted" calculations of \( R_{\mathrm{a}} \) and \( R_{\mathrm{b}} \).

The supply voltage is simply the product of the supply current and total resistance.

\( V_{\mathrm{s}} = I_{\mathrm{s}} R_{\mathrm{T}} = 8.5 \cdot 45.4118 \) = 386 V #.