Electromagnetism Resource
4. Electromagnetic Effects
4.3. Force Between Two Current-Carrying Conductors
As noted previously, a current-carrying conductor in a magnetic field experiences a force given by:
\( F = B i L \sin \theta \).
So far, a permanent magnet has been considered as the source of that magnetic field.
However, it is possible for the source of the magnetic field to be another current-carrying wire.
In this course, we will consider the force between parallel current-carrying wires.
If the wires are parallel, the magnetic field from one wire passing through another will always be at right angles.
Therefore, the equation for the force can be simplified to:
\( F = B i L \).
Analysis
The images show two long, parallel wires. The \( \otimes \) and \( \odot \) symbols represent the current going into or coming out of the screen surface respectively.
Since there are two wires, there are two sets of magnetic fields.
Note that a given conductor is not affected by its own magnetic field. The force comes from the combination of the conductor's current and the other conductor's magnetic field.
| Description | Symbol - Conductor 1 |
Symbol - Conductor 2 |
|---|---|---|
| Force on a particular conductor (N) |
\( F_{12} \) |
\( F_{21} \) |
| Magnetic field due to that particular conductor (T) |
\( B_1 \) |
\( B_2 \) |
| Current in a conductor (A) |
\( i_1 \) | \( i_1 \) |
The conductors are spaced \( d \) metres apart (not shown on the drawings).
If the currents in the wires are going in the same directions, the wires will attract each other.
The image below shows both currents going away from you.
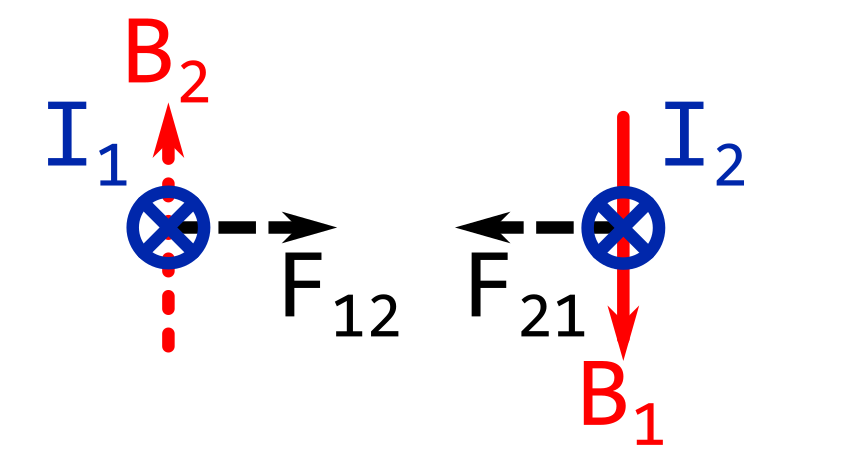
The image below shows both currents going towards you.
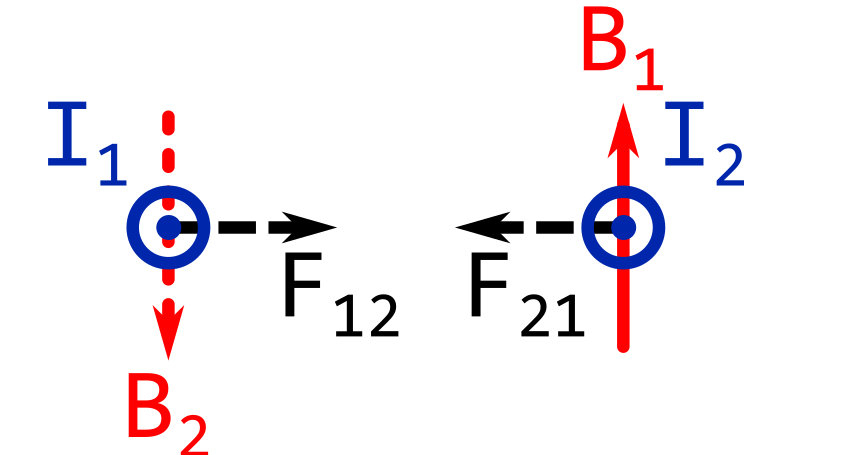
If the currents in the wires are going in the opposite directions, the wires will repel each other.
The image below shows \( I_1 \) going away from you.
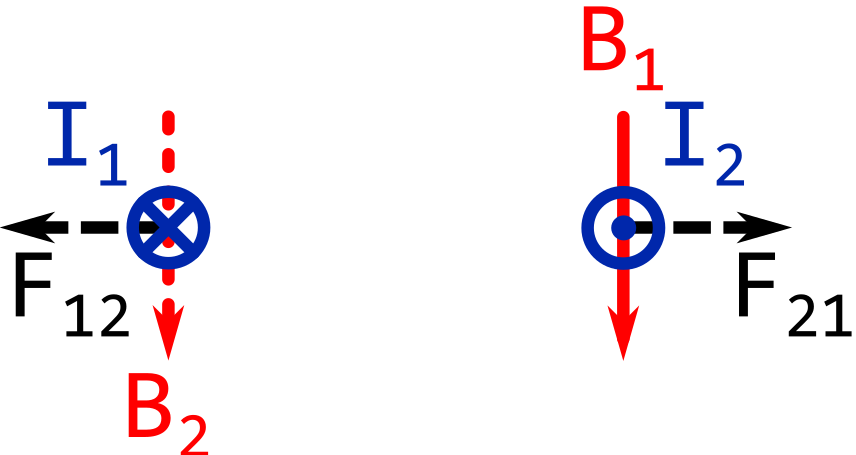
The image below shows \( I_1 \) going towards you.
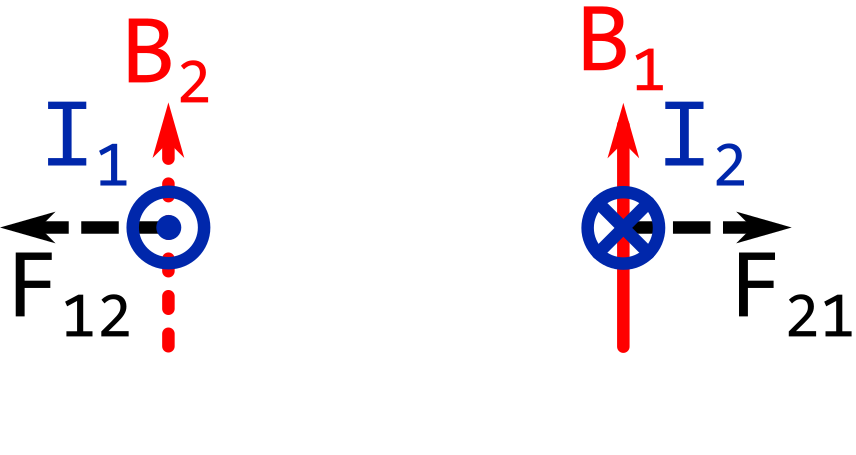
The force between the conductors is mutual. The conductors are pushed away from (or pulled towards) each other.
It is easier to see the force when the wires start moving when the current is first applied.
The first "half swing" will tell you whether the nature of the force.
If the wires swing away from each other, the force is repulsive. If the wires swing towards each other, the force is attractive.
Force Calculation
The basic equation for the force is:
\( F = B i L \)
But the magnetic field is known, as it comes from the other conductor.
The magnetic field around a long, straight current-carrying conductor is given by:
\( B = \frac{\mu_0 \mu_{\mathrm{r}} i}{2 \pi d} \)
where \( B \) is the magnetic flux density (T), \( \mu_0 \) is the permeability of free space (H.m-1), \( \mu_{\mathrm{r}} \) is the relative permeability of the medium surrounding the conductor (dimensionless), \( i \) is the current through the conductor (A), and \( d \) is the radial distance from the conductor (m).
Given that \( \mu_0 \) is approximately (to about 1 part in 1 billion) \( 4 \pi \cdot 10^{-7} \), the magnetic field equation can be simplified further.
\( B = 2 \cdot 10^{-7} \cdot \frac{\mu_{\mathrm{r}} i}{d} \)
The force seen by conductor 1 is:
\( F_{12} = B_2 i_1 L = 2 \cdot 10^{-7} \cdot \frac{\mu_{\mathrm{r}} i_1 i_2}{d} \)
The force seen by conductor 1 is:
\( F_{21} = B_1 i_2 L = 2 \cdot 10^{-7} \cdot \frac{\mu_{\mathrm{r}} i_1 i_2}{d} \)
Note these forces are both the same magnitude.
If the current in both wires is the same, the force equation simplifies to:
\( F = 2 \cdot 10^{-7} \cdot \frac{\mu_{\mathrm{r}} i^2}{d} \)
For wires suspended in air, the forces are fairly small, and care is needed to observe the force.
For example, suppose two 1 m long wires are suspended 0.1 m apart in air (\( \mu_{\mathrm{r}} = \) 1), and are carrying 10 A in opposite directions.
The force is calculated below.
\( F = 2 \cdot 10^{-7} \cdot \frac{i^2 L}{d} = 2 \cdot 10^{-7} \cdot \frac{10^2}{0.1} = \) 0.0002 N.
Since the currents are flowing in opposite directions, the force is repulsive. Note that the force is quite small. The force is the same as the weight of an item with a mass of 20.3 µg.
The forces are made larger with higher permeability magnetic materials, having multiple turns of wire, and closer spacings.