Previous
Next

6. AC Electricity

6.1. Sine Waveforms

We have already seen that the output from an AC generator uses the \( \sin \) function.

There are two functions that form a sine wave:

  • sine, denoted \( \sin \);
  • cosine, denoted \( \cos \).

Sine and Cosine Definitions

The sine and cosine functions are orthogonal in the sense that any sinusoid or sinusoidal wave can be expressed as the sum of a sine wave and a cosine wave.

The sine and cosine waveforms are shown below for a single cycle.

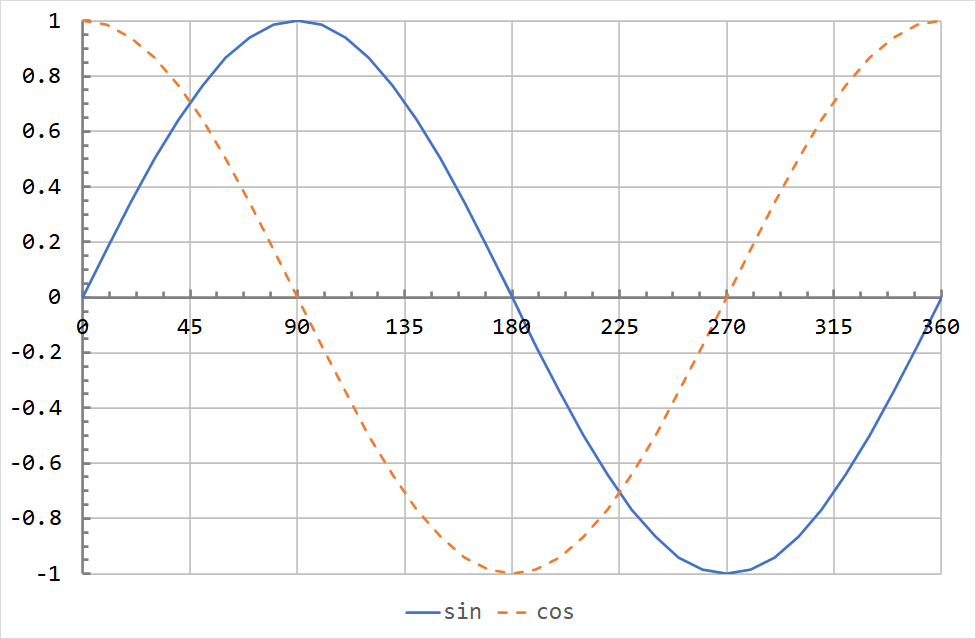
Sine and Cosine

As can be seen, the sine and cosine waves have identical shapes. Sinusoids have a property called phase, which determines the horizontal offset from a reference wave.

For sine waves and cosine waves, some useful relationships are shown below:

  1. \( \cos(-\theta) = \cos(\theta) \): cosine is an even function, in the sense that it has symmetry around \( \theta = 0 \).
  2. \( \sin(-\theta) = -\sin(\theta) \): sine is an odd function, in the sense that it has anti-symmetry around \( \theta = 0 \).
  3. \( \cos \theta = \sin(90^{\circ} - \theta) \): the "standard" cosine-sine conversion.
  4. \( \sin \theta = \cos(90^{\circ} - \theta) \): the "standard" sine-cosine conversion.
  5. \( \cos \theta = -\sin(\theta - 90^{\circ}) \): similar to #3, except \( \theta \) is made positive.
  6. \( \sin \theta = \cos(\theta - 90^{\circ}) \): similar to #4, except \( \theta \) is made positive.
  7. \( \sin \theta = \sin(\theta + n \cdot 360^{\circ}) \): sinusoids are periodic, with a period of 360°. This also applies to cosine waves.
  8. \( \sin(\theta + \phi) = \sin\theta \sin \phi + \cos \theta \cos \phi \): every sine wave with a phase shift can be decomposed into the sum of a sine wave and a cosine wave.
  9. \( \cos(\theta + \phi) = \cos\theta \cos \phi - \sin \theta \sin \phi \): every cosine wave with a phase shift can be decomposed into the sum of a cosine wave and a sine wave.

A parametric plot of sine and cosine shown below. The x-axis is horizontal, and the y-axis is vertical. The parametric plot coordinates are \( (x, y) = (\cos\theta, \sin\theta) \). In other words, it is the graph above, but with the functions plotted against each other, rather than angle. The plot begins at (1, 0) (the far right) and proceeds in a circle anti-clockwise.

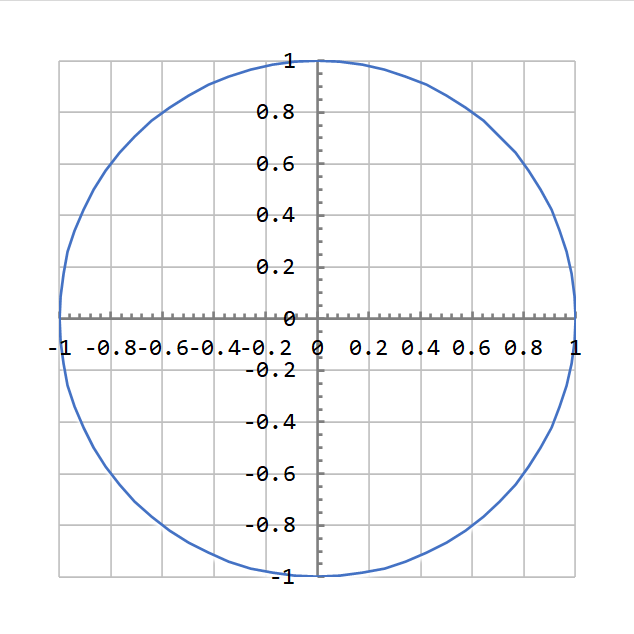
cosine-sine parametric plot

The parametric plot implies one more important identity:

  • \( \sin^2 \theta + \cos^2 \theta = 1 \).

Using Radians

In circuit analysis, it is more common to work with angles in radians. Using radians makes the expression of a sine wave as a function of frequency very simple.

The rules above apply as below for radians:

  1. \( \cos(-\theta) = \cos(\theta) \): no difference from above.
  2. \( \sin(-\theta) = -\sin(\theta) \): no difference from above.
  3. \( \cos \theta = \sin(\frac{\pi}{2} - \theta) \): the "standard" cosine-sine conversion.
  4. \( \sin \theta = \cos(\frac{\pi}{2} - \theta) \): the "standard" sine-cosine conversion.
  5. \( \cos \theta = -\sin(\theta - \frac{\pi}{2}) \): similar to #3, except \( \theta \) is made positive.
  6. \( \sin \theta = \cos(\theta - \frac{\pi}{2}) \): similar to #4, except \( \theta \) is made positive.
  7. \( \sin \theta = \sin(\theta + 2 \pi n) \): sinusoids are periodic, with a period of \( 2 \pi \). This also applies to cosine waves.
  8. \( \sin(\theta + \phi) = \sin\theta \sin \phi + \cos \theta \cos \phi \): no difference from above.
  9. \( \cos(\theta + \phi) = \cos\theta \cos \phi - \sin \theta \sin \phi \): no difference from above.

For convenience, a phase shift may be written in degrees anyway e.g. \( \cos (\theta + 45^{\circ}) \). You must remember to convert the phase shift to radians before doing any calculations.

Sinusoids in Circuit Analysis

Sinusoids in circuit analysis are usually expressed in the following forms:

  • \( u(t) = A \sin (2 \pi f t + \phi) \); and
  • \( u(t) = A \cos (2 \pi f t + \phi) \)

where:

  • \( A \) is the amplitude, or peak of the sinusoid;
  • \( f \) is the frequency (Hz);
  • \( t \) is time (s);
  • and \( \phi \) is the phase shift.

The sine and cosines in the formula above use radians as the angle unit. There are \( 2 \pi \) (≈ 6.283) radians in a full revolution, or 1 rad ≈ 57.296°, or 1° ≈ 0.01745 rad.

The factor \( 2 \pi f \) may be factored into angular frequency \( \omega \) (small Greek letter omega). The unit of \( \omega \) is rad.s-1. Using \( \omega \) changes the expressions to:

  • \( u(t) = A \sin (\omega t + \phi) \); and
  • \( u(t) = A \cos (\omega t + \phi) \)

The waveforms may also be expressed using the period or cycle length of the wave. The period is denoted \( T \) and is the time required for one cycle of the wave. The unit of the period is s.

The relationship between the period and frequency is:

\( f = \frac{1}{T} \)

where \( f \) is the frequency (Hz), and \( T \) is the period (s).

Previous
Next