Worksheet 6A - Parallel Circuit Calculations - Solutions and Commentary
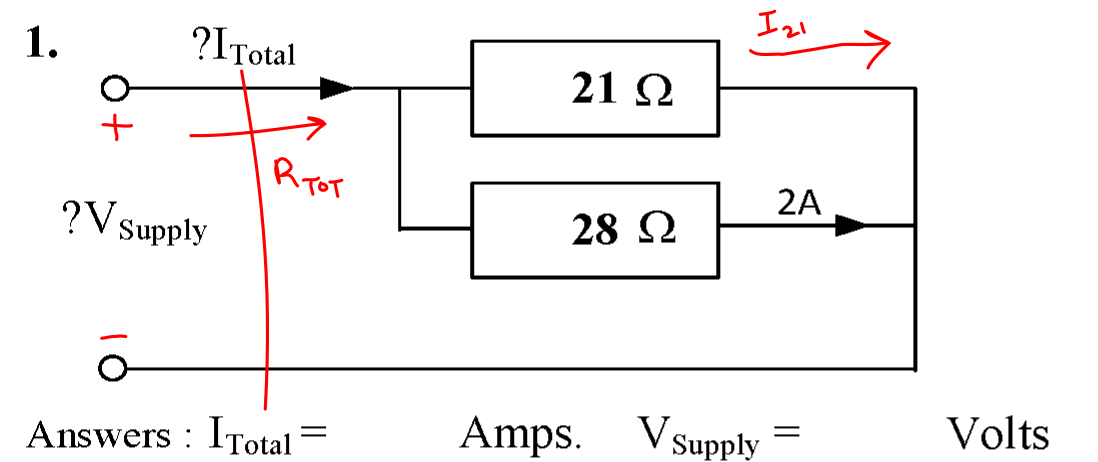
Question 1
The objective of this question is to work out:
- The supply voltage \( V_{\mathrm{Supply}} \).
- The supply voltage \( I_{\mathrm{Total}} \).
The circuit is shown below.
Solution - Method 1
The supply voltage is the same as the voltage drops across the resistors. In this case, we know that the 28 Ω resistor has 2 A flowing through it.
\( V_{\mathrm{Supply}} = 2 \cdot 28 \) = 56 V #.
The current is the 2 A flow through the 28 Ω resistor plus the current drawn by the 21 Ω resistor from the 56 V supply.
\( I_{\mathrm{Total}} = 2 + \frac{56}{21} = \frac{14}{3} \) = 4.67 A (2 dp) #.
Solution - Method 2
The supply voltage is the same as the voltage drops across the resistors. In this case, we know that the 28 Ω resistor has 2 A flowing through it.
\( V_{\mathrm{Supply}} = 2 \cdot 28 \) = 56 V #.
The total resistance \( R_{\mathrm{TOT}} \) is calculated.
\( R_{\mathrm{TOT}} = (21^{-1} +28^{-1})^{-1} \) = 12 Ω.
The supply current is then calculated.
\( I_{\mathrm{Total}} = \frac{56}{12} = \frac{14}{3} \) = 4.67 A (2 dp) #.
Solution - Method 3
The supply voltage is the same as the voltage drops across the resistors. In this case, we know that the 28 Ω resistor has 2 A flowing through it.
\( V_{\mathrm{Supply}} = 2 \cdot 28 \) = 56 V #.
The current is the 2 A flow through the 28 Ω resistor plus the current drawn by the 21 Ω resistor from the 56 V supply.
The current drawn by the 21 Ω resistor will be exactly \( \frac{28}{21} \) times the current drawn by the 28 Ω resistor. This behaviour comes from Ohm's Law. The derivation is below.
\( I_{21} = \frac{V_{\mathrm{Supply}}}{21} = \frac{V_{\mathrm{Supply}}}{28} \cdot \frac{28}{21} \)
The total current can then be calculated.
\( I_{\mathrm{Total}} = 2 + 2 \cdot \frac{28}{21} = \frac{14}{3} \) = 4.67 A (2 dp) #.
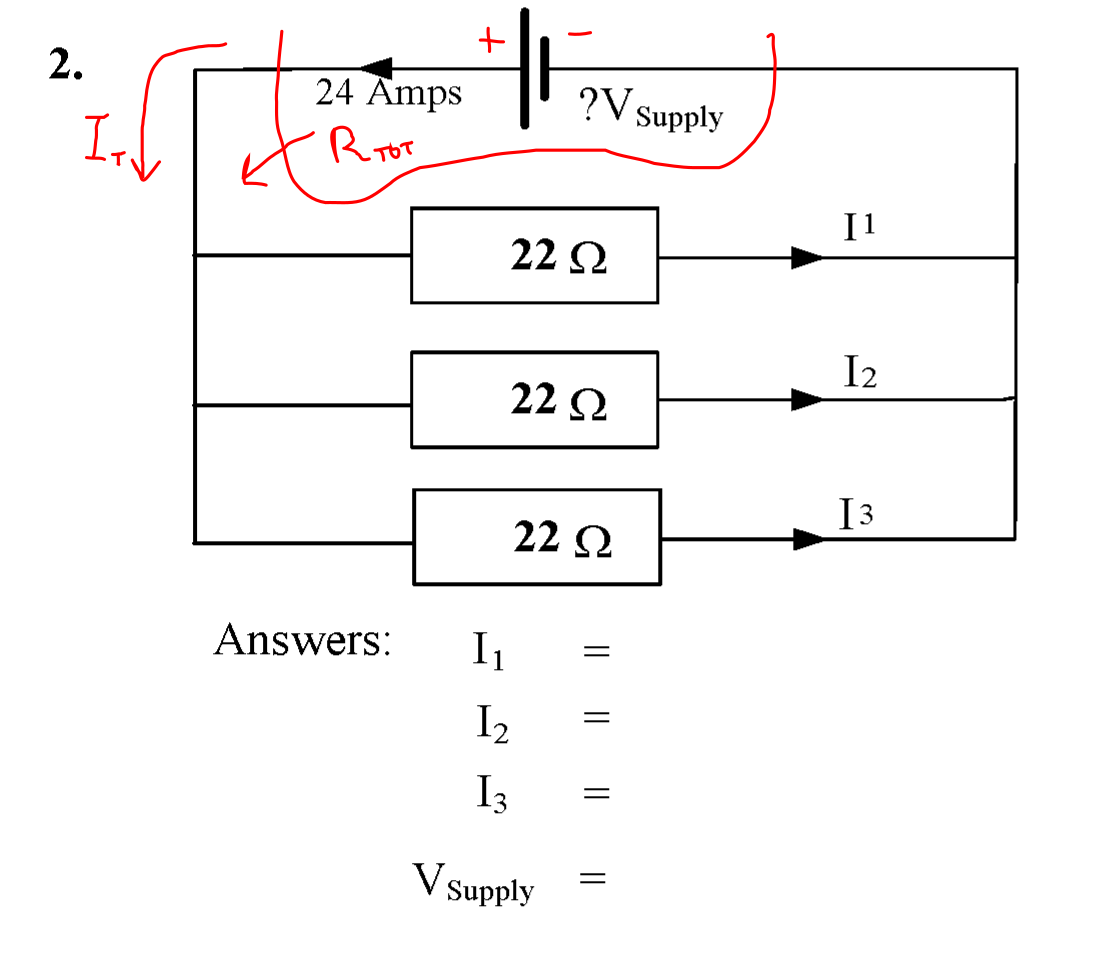
Question 2
The objective of this question is to work out the following quantities:
- The current through the 22 Ω resistor \( I_1 \);
- The current through the 22 Ω resistor \( I_2 \);
- The current through the 22 Ω resistor \( I_3 \);
- The supply voltage total circuit current \( V_{\mathrm{Supply}} \).
The circuit is shown below.
Solution - Method 1
The three resistors are all the same value. Therefore, the current will divide equally among them.
\( I = I_{\mathrm{T}} \cdot \frac{R_{\mathrm{TOT}}}{R} = I_{\mathrm{T}} \cdot \frac{\left ( \frac{R}{3} \right) }{R} = I_{\mathrm{T}} \cdot \frac{1}{3} \)
Using this formula, we get the following results.
- \( I_1 = \frac{I_{\mathrm{T}}}{3} \) = 8 A #.
- \( I_2 = I_1 \) = 8 A #.
- \( I_3 = I_2 = I_1 \) = 8 A #.
The supply voltage \( V_{\mathrm{Supply}} \) is just \( I_n R_n \), where \( n \) stands for any one of the resistors and the current through them. It does not matter which, because all the resistances and currents are the same.
\( V_{\mathrm{Supply}} = I_n R_n = 8 \cdot 22 \) = 176 V #.
Solution - Method 2
The supply voltage can be calculated from Ohm's Law on the total resistance \( R_{\mathrm{TOT}} \) and the known supply current \( I_{\mathrm{T}} \) of 24 A.
\( R_{\mathrm{TOT}} = (22^{-1} + 22^{-1} + 22^{-1})^{-1} = \frac{22}{3} = \frac{22}{3}\) Ω.
The supply voltage \( V_{\mathrm{Supply}} \) is just \( I_{\mathrm{T}} R_{\mathrm{TOT}} \).
\( V_{\mathrm{Supply}} = I_{\mathrm{T}} R_{\mathrm{TOT}} = 24 \cdot \frac{22}{3} \) = 176 V (3 sf) #.
The three resistors are all the same value. Therefore, the current will divide equally among them.
\( I = I_{\mathrm{T}} \cdot \frac{R_{\mathrm{TOT}}}{R} = I_{\mathrm{T}} \cdot \frac{\left( \frac{R}{3} \right)}{R} = I_{\mathrm{T}} \cdot \frac{1}{3} \)
Using this formula, we get the following results.
- \( I_1 = \frac{I_{\mathrm{T}}}{3} \) = 8 A #.
- \( I_2 = I_1 \) = 8 A #.
- \( I_3 = I_2 = I_1 \) = 8 A #.
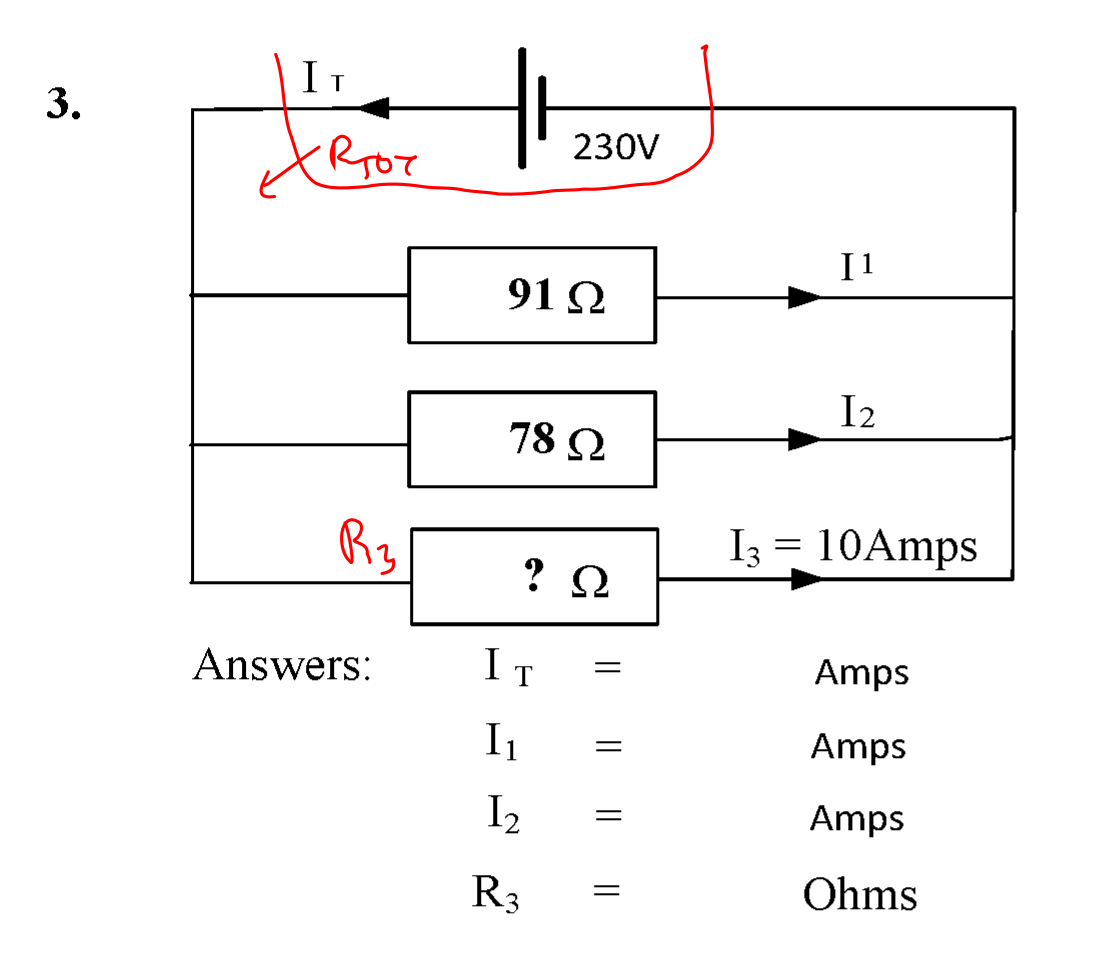
Question 3
The objective of this question is to work out the following quantities:
- The total circuit current \( I_{\mathrm{T}} \);
- The unknown resistor \( R_3 \).
The circuit is shown below.
Solution - Method 1
The unknown resistance \( R_3 \) is calculated using Ohm's Law.
\( R_3 = \frac{230}{10} \) = 23 Ω #.
The total current can be calculated using Ohm's Law on the known resistors. First, the unknown currents \( I_1 \) and \( I_2 \) are calculated.
- \( I_1 = \frac{230}{91} \) = 2.53 A (2 dp) #.
- \( I_2 = \frac{230}{78} = \frac{115}{39} \) = 2.95 A (2 dp) #.
The total current is the sum of these three branch currents.
\( I_{\mathrm{T}} = I_1 + I_2 + I_3 = \frac{230}{91} + \frac{115}{39} + 10 = \frac{325}{21} \) = 15.48 A (2 dp) #.
Solution - Method 2
The total current can be calculated using Ohm's Law on the known resistors. First, the unknown currents \( I_1 \) and \( I_2 \) are calculated.
- \( I_1 = \frac{230}{91} \) = 2.53 A (2 dp) #.
- \( I_2 = \frac{230}{78} = \frac{115}{39} \) = 2.95 A (2 dp) #.
The total current is the sum of these three branch currents.
\( I_{\mathrm{T}} = I_1 + I_2 + I_3 = \frac{230}{91} + \frac{115}{39} + 10 = \frac{325}{21} \) = 15.48 A (2 dp) #.
The total resistance \( R_{\mathrm{TOT}} \) is calculated using Ohm's Law.
\( R_{\mathrm{TOT}} = \frac{230}{\left( \frac{325}{21} \right)} = 230 \cdot \frac{21}{325} = \frac{966}{65} \) = 14.862 Ω (5 sf).
The parallel resistance formula can be used to extract the unknown resistance \( R_3 \).
\( \frac{65}{966} = \frac{1}{91} + \frac{1}{78} + \frac{1}{R_3} \rightarrow \frac{1}{R_3} = \frac{65}{966} - \frac{1}{91} - \frac{1}{78} \)
R_3 can be calculated.
\( \frac{1}{R_3} = \frac{1}{23} \rightarrow R_3 \) = 23 Ω.
Question 4
The objective of this question is to work out the following quantities:
- The current through the 5 Ω resistor \( I_1 \);
- The current through the 12 Ω resistor \( I_2 \);
- The current through the 20 Ω resistor \( I_3 \);
- The total circuit current \( I_{\mathrm{T}} \);
- The total resistance \( R_{\mathrm{T}} \).
The circuit is shown below.

We are given that the voltage across the "upper" leg of the 20 Ω resistor (considered "upper" as its voltage is more positive) and the lower leg of the 12 Ω resistor is 7 V.
NOTE: The voltage across any set of parallel set of components is the same.
Solution - Method 1
This circuit can be solved with Ohm's Law and Kirchhoff's Current Law in that order.
First, calculate the resistor currents.
- \( I_1 = \frac{7}{5} \) = 1.4 A #.
- \( I_2 = \frac{7}{12} \) = 0.583 A (3 sf) #.
- \( I_3 = \frac{7}{20} \) = 0.35 A #.
The total current is the sum of these three branch currents.
\( I_{\mathrm{T}} = I_1 + I_2 + I_3 = \frac{7}{5} + \frac{7}{12} + \frac{7}{20} = \frac{7}{3} \) = 2.33 A (3 sf) #.
The total resistance may be calculated using Ohm's Law.
\( R_{\mathrm{T}} = \frac{7}{\left( \frac{7}{3} \right)} = 7 \cdot \frac{3}{7} \) = 3 Ω #.
Solution - Method 2
The resistance the 7 V voltage appears across is the total resistance of the three resistors.
\( R_{\mathrm{T}} = (5^{-1} + 12^{-1} + 20^{-1})^{-1} \) = 3 Ω.
The supply current is calculated by dividing the parallel circuit voltage by \( R_{\mathrm{T}} \).
\( I_{\mathrm{T}} = \frac{7}{3} \) = 2.33 A # (3 sf).
The resistor currents can also be calculated.
- \( I_1 = \frac{7}{5} \) = 1.4 A #.
- \( I_2 = \frac{7}{12} \) = 0.583 A (3 sf) #.
- \( I_3 = \frac{7}{20} \) = 0.35 A #.
The resistance the 7 V voltage appears across is the total resistance of the three resistors.
\( R_{\mathrm{T}} = (5^{-1} + 12^{-1} + 20^{-1})^{-1} \) = 3 Ω.
The supply current is calculated by dividing the supply voltage by \( R_{\mathrm{T}} \).
\( I_{\mathrm{T}} = \frac{7}{3} \) = 2.33 A # (3 sf).
The resistor currents can also be calculated using current division \( I = I_{\mathrm{T}} \cdot \frac{R_{\mathrm{T}}}{R} \).
- \( I_1 = 15 \cdot \frac{3}{5} \) = 9 A #.
- \( I_2 = 15 \cdot \frac{3}{12} \) = 3.75 A #.
- \( I_3 = 15 \cdot \frac{3}{20} \) = 2.25 A #.
Question 5
The objective of this question is to work out the following quantities:
- The current through the 35 Ω resistor \( I_1 \);
- The current through the 14 Ω resistor \( I_2 \);
- The total circuit current \( I_{\mathrm{T}} \).
The circuit is shown below.

NOTE: The order of elements in a parallel circuit does not matter! There are no special steps you need to take to in your calculations just because the voltage source is in the "middle" of the circuit.
Solution - Method 1
This circuit can be solved with Ohm's Law and Kirchhoff's Current Law in that order.
First, calculate the resistor currents.
- \( I_1 = \frac{25}{35} \) = 0.7143 A (4 dp) or 0.71 A (2dp) #.
- \( I_2 = \frac{25}{14} \) = 1.7857 A (4 dp) or 1.79 A (2 dp) #.
The total current is the sum of these three branch currents.
\( I_{\mathrm{T}} = I_1 + I_2 = 0.7143 + 1.7857 \) = 2.5 A #.
Solution - Method 2
The resistance as seen by the 25 V voltage source is the total resistance of the two resistors.
\( R_{\mathrm{TOT}} = (35^{-1} + 14^{-1})^{-1} \) = 10 Ω.
The supply current is calculated by dividing the supply voltage by \( R_{\mathrm{TOT}} \).
\( I_{\mathrm{T}} = \frac{25}{10} \) = 2.5 A #.
The resistor currents can also be calculated.
- \( I_1 = \frac{25}{35} \) = 0.71 A (2 dp) #.
- \( I_2 = \frac{25}{14} \) = 1.79 A (2 dp) #.
The resistance as seen by the 25 V voltage source is the total resistance of the two resistors.
\( R_{\mathrm{TOT}} = (35^{-1} + 14^{-1})^{-1} \) = 10 Ω.
The supply current is calculated by dividing the supply voltage by \( R_{\mathrm{TOT}} \).
\( I_{\mathrm{T}} = \frac{25}{10} = \frac{5}{2} \) = 2.5 A #.
The resistor currents can also be calculated using current division \( I = I_{\mathrm{TOT}} \cdot \frac{R_{\mathrm{TOT}}}{R} \).
- \( I_1 = \frac{5}{2} \cdot \frac{10}{35} = \frac{5}{7} \) = 0.71 A (2 dp) #.
- \( I_2 = \frac{5}{2} \cdot \frac{10}{14} = \frac{25}{14} \) = 1.79 A (2 dp) #.