Worksheet 10B - Total Resistance Network - Solutions and Commentary
General Notes
These questions have parallel resistance circuits.
The general formula for the total resistance \( R_{\mathrm{T}} \) of parallel resistance circuit is shown below.
The general formulas have some different notations:
\( R_{\mathrm{T}} = \frac{1}{\sum \frac{1}{R}} \)
\( R_{\mathrm{T}} = \frac{1}{\sum R^{-1}} \)
\( R_{\mathrm{T}} = \left( \sum R^{-1} \right)^{-1} \)
\( \frac{1}{R_{\mathrm{T}}} = \frac{1}{R_1} + \frac{1}{R_2} \ldots \)
\( R_{\mathrm{T}} = R_1 \parallel R_2 \parallel R_3 \parallel \ldots \)
where \( R_{\mathrm{T}} \) is the total parallel resistance, the sum symbol \( \sum \) represents a summation, and \( R \) is a resistor in the parallel circuit.
Question 1
The circuit is shown below.
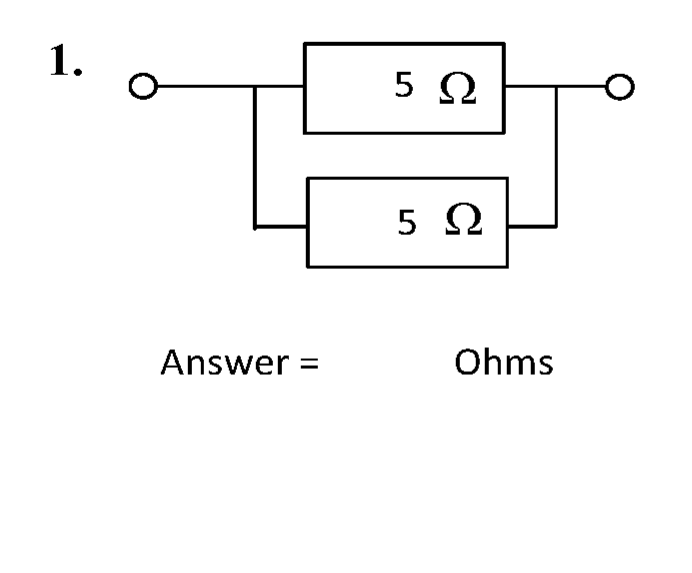
Solution - Method 1
The total resistance \( R_{\mathrm{T}} \) is simply the parallel combination of these resistors.
\( R_{\mathrm{T}} = 5 \parallel 5 = \left (\sum R^{-1} \right) ^{-1} = (5^{-1} + 5^{-1})^{-1} \) = 2.5 Ω #.
Solution - Method 2
The two resistors have identical values. This is special case of the parallel resistance formula.
If there are \( n \) identical value parallel resistors, the parallel resistance formula reduces to:
\( R_{\mathrm{T}} = \frac{R}{n} \)
where \( R_{\mathrm{T}} \) is the total parallel resistance, and \( R \) is a resistor in the parallel circuit.
Using this special case, we can solve the circuit. There are two resistors of 5 Ω, so \( R = 5 \), and \( n = 2 \).
\( R_{\mathrm{T}} = \frac{5}{2} \) = 2.5 Ω #.
Question 2
The circuit is shown below.
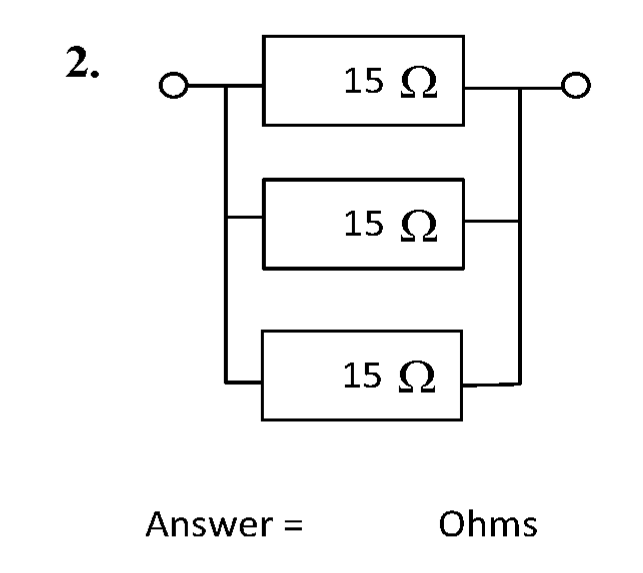
Solution - Method 1
The total resistance \( R_{\mathrm{T}} \) is simply the parallel combination of these resistors.
\( R_{\mathrm{T}} = 15 \parallel 15 \parallel 15 = \left (\sum R^{-1} \right) ^{-1} = (15^{-1} + 15^{-1} + 15^{-1})^{-1} \) = 5 Ω #.
Solution - Method 2
The three resistors have identical values. This is special case of the parallel resistance formula.
Using the identical parallel resistances formula (see Question 1) we can solve the circuit. There are three resistors of 15 Ω, so \( R = 15 \), and \( n = 3 \).
\( R_{\mathrm{T}} = \frac{15}{3} \) = 5 Ω #.
Question 3
The circuit is shown below.
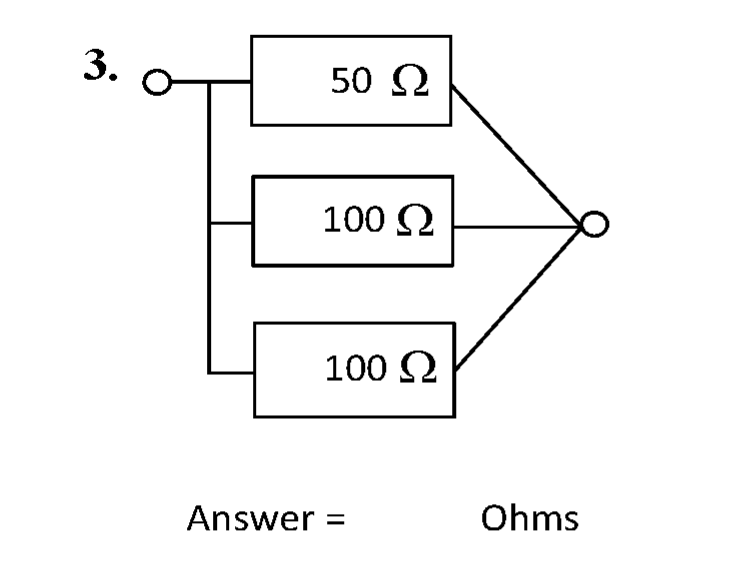
The left-hand side connection is a "bus" connection. The right hand side connection is a "star" connection. The nature of these connections has no effect on the parallel resistance.
Solution - Method 1
The total resistance \( R_{\mathrm{T}} \) is simply the parallel combination of these resistors.
\( R_{\mathrm{T}} = 50 \parallel 100 \parallel 100 = \left (\sum R^{-1} \right) ^{-1} = (50^{-1} +100^{-1} + 100^{-1})^{-1} \) = 25 Ω #.
Solution - Method 2
We can think of this circuit as two 100 Ω resistors in parallel a 50 Ω resistor.
Using the identical parallel resistances formula (see Question 1) we can solve for the two 100 Ω resistors in parallel. The answer is 50 Ω.
The circuit is now equivalent to two 50 Ω resistors in parallel.
\( R_{\mathrm{T}} = \frac{50}{2} \) = 25 Ω #.
Solution - Method 3
We can think of this circuit as two 100 Ω resistors in parallel a 50 Ω resistor.
We can do come algebra on the parallel operator (\( \parallel \)) to "pre-simplify" our expression.
\( R_{\mathrm{T}} = 50 \parallel 100 \parallel 100 \).
The parallel operator is associative, in other words you can "precompute" parts of the expression before doing the "final" calculation.
\( R_{\mathrm{T}} = 50 \parallel 100 \parallel 100 = 50 \parallel (100 \parallel 100) \).
The parallel combination of two equal value resistors is half the value of the original resistor i.e. \( 100 \parallel 100 = \frac{100}{2} = 50 \).
\( R_{\mathrm{T}} = 50 \parallel 50 \).
The parallel combination of two equal value resistors is half the value of the original resistor i.e. \( 50 \parallel 50 = 25 \).
\( R_{\mathrm{T}} = 50 \parallel 50 = \frac{50}{2} \) = 25 Ω #.
Question 4
The circuit is shown below.
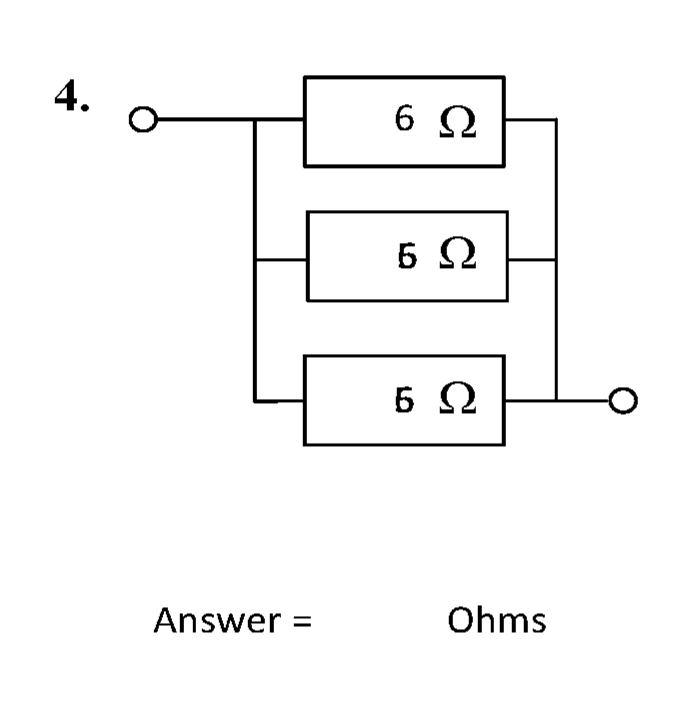
The left-hand side and right-hand side connections are both "bus" connections. The component the terminals are most "directly" connected to makes no difference to the total resistance.
Solution - Method 1
The total resistance \( R_{\mathrm{T}} \) is simply the parallel combination of these resistors.
\( R_{\mathrm{T}} = \left (\sum R^{-1} \right) ^{-1} = (6^{-1} + 6^{-1} + 6^{-1})^{-1} \) = 2 Ω #.
Solution - Method 2
The three resistors have identical values. This is special case of the parallel resistance formula.
Using the identical parallel resistances formula (see Question 1) we can solve the circuit. There are three resistors of 6 Ω, so \( R = 6 \), and \( n = 3 \).
\( R_{\mathrm{T}} = \frac{6}{3} \) = 2 Ω #.
Question 5
The circuit is shown below.
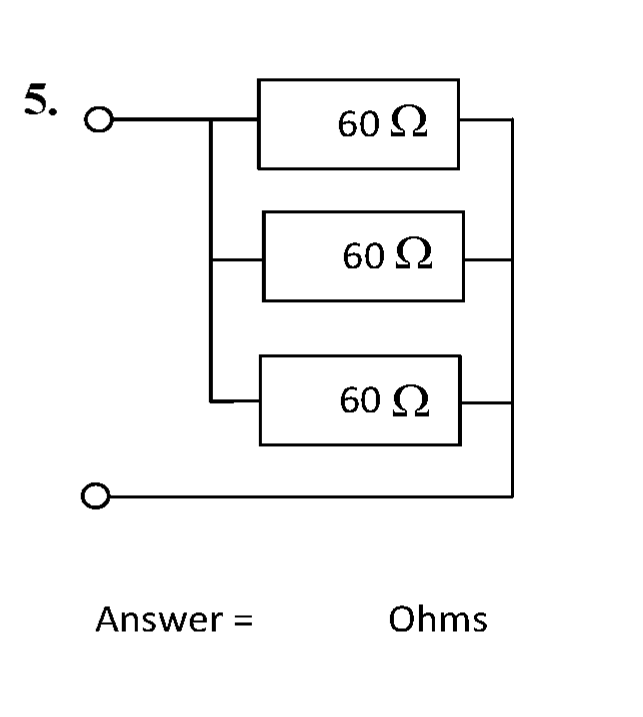
The left-hand side and right-hand side connections are both "bus" connections. The component the terminals are most "directly" connected to makes no difference to the total resistance.
Solution - Method 1
The total resistance \( R_{\mathrm{T}} \) is simply the parallel combination of these resistors.
\( R_{\mathrm{T}} = \left (\sum R^{-1} \right) ^{-1} = (60^{-1} + 60^{-1} + 60^{-1})^{-1} \) = 20 Ω #.
Solution - Method 2
The three resistors have identical values. This is special case of the parallel resistance formula.
Using the identical parallel resistances formula (see Question 1) we can solve the circuit. There are three resistors of 60 Ω, so \( R = 60 \), and \( n = 3 \).
\( R_{\mathrm{T}} = \frac{60}{3} \) = 20 Ω #.
Question 6
The circuit is shown below.
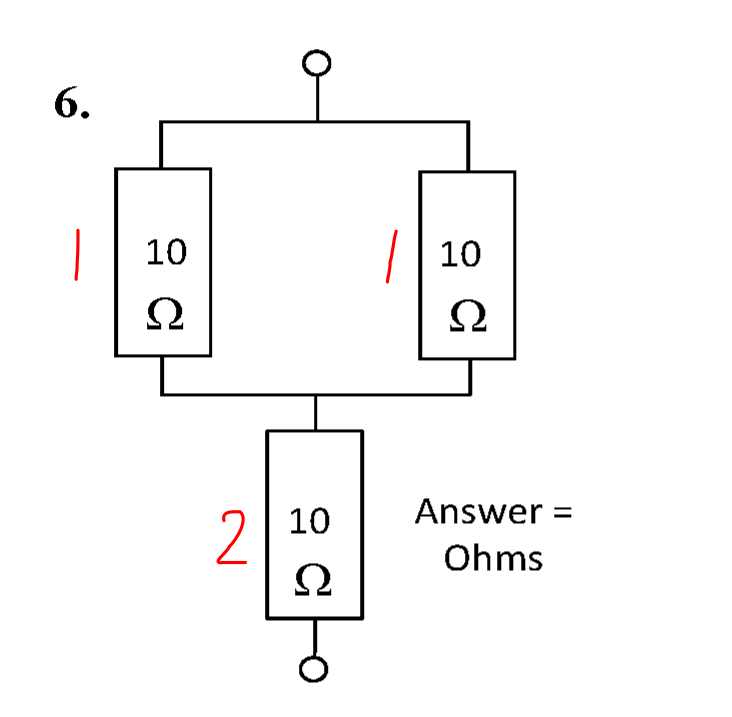
This circuit is a mixed series and parallel circuit. The resistors are grouped into sets that can be treated like individual series or parallel resistors.
When solving a mixed series and parallel circuit, do not mix series and parallel groups of resistors in your calculations. In other words, do not treat the circuit above as two 20 Ω resistors in parallel.
It is essential to understand that groups of resistors can only be combined if:
- The resistors would have the same current flowing through them (i.e. series circuit).
- The resistors would have the same voltage drop across them (i.e. parallel circuit).
Solution - Method 1
In order to combine the resistors, the parallel resistance of group 2 (\( R_2 \)) must be calculated.
\( R_2 = \frac{10}{2} \) = 5 Ω.
The circuit then becomes as below.
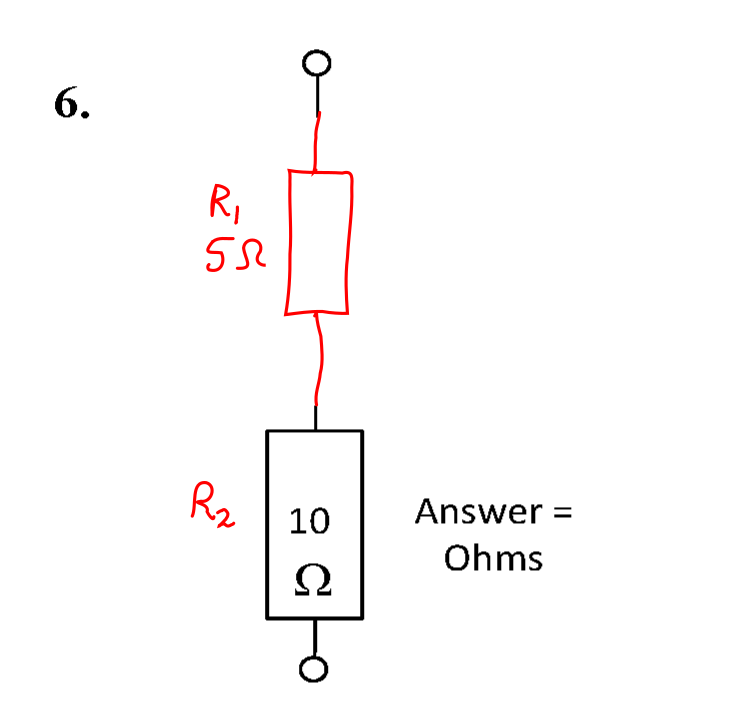
The problem may now be solved as a simple series circuit.
\( R_{\mathrm{T}} = \sum R = 5 + 10 \) = 15 Ω #.
Solution - Method 2
The expression for the total resistance \( R_{\mathrm{T}} \) can be constructed by direct inspection of the circuit. We have a 10 Ω resistor in series with two 10 Ω resistors in parallel.
\( R_{\mathrm{T}} = 10 + 10 \parallel 10 \)
The parallel operator always has higher priority than addition or subtraction. Knowing, this, we can calculate \( R_{\mathrm{T}} \).
\( R_{\mathrm{T}} = 10 + 10 \parallel 10 = 10 + 5 \) = 15 Ω #.
Note that the following operations will not result in the same answer.
- \( 10 + 10 \parallel 10 \neq (10 + 10) \parallel 10 \).
- \( 10 + 10 \parallel 10 \neq 10 \parallel (10 + 10) \).
- \( 10 + 10 \parallel 10 \neq (10 + 10) \parallel (10 + 10) \).
In other words, series and parallel circuits must be treated separately. You cannot mix them in calculations like that shown above.
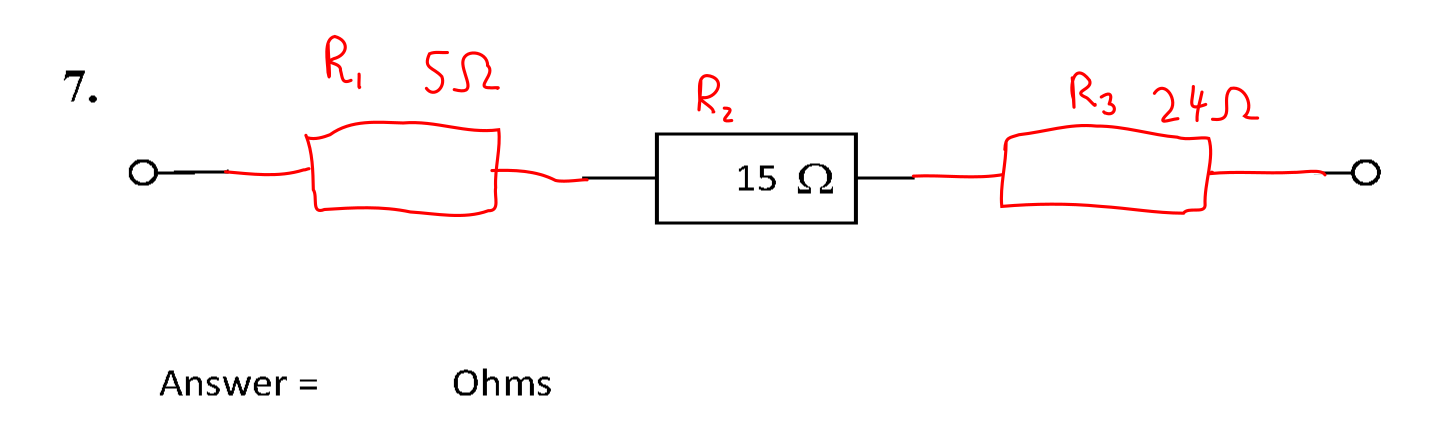
Question 7
The circuit is shown below.
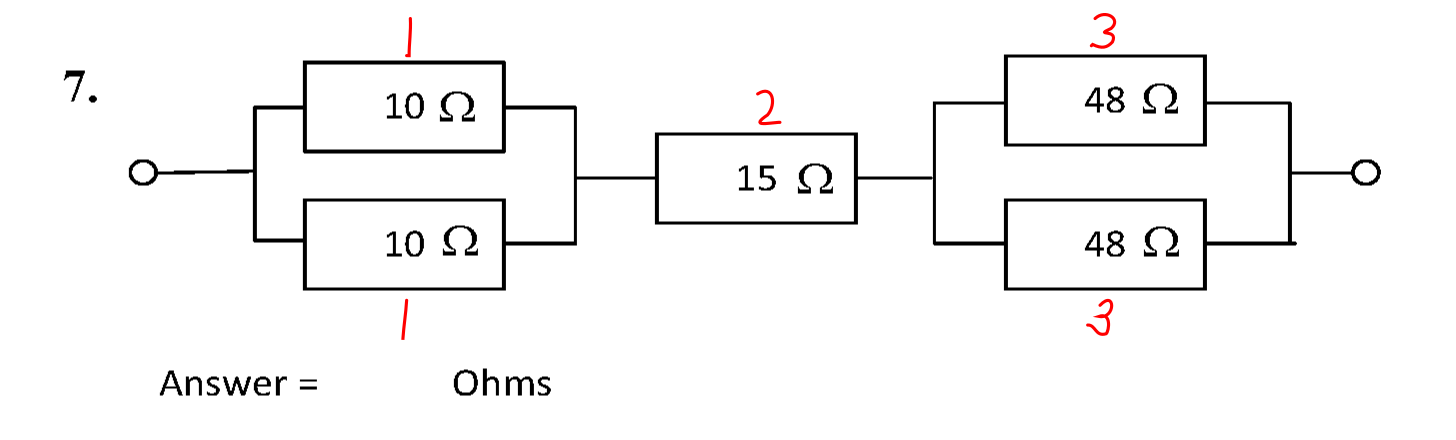
This circuit is a mixed series and parallel circuit. The resistors are grouped into sets that can be treated like individual series or parallel resistors.
Solution - Method 1
In order to combine the resistors, the parallel resistances of groups 1 (\( R_1 \)) and 3 (\( R_3 \)) must be calculated.
- \( R_1 = \frac{10}{2} \) = 5 Ω.
- \( R_3 = \frac{48}{2} \) = 24 Ω.
The circuit then becomes as below.
The problem may now be solved as a simple series circuit.
\( R_{\mathrm{T}} = \sum R = 5 + 15 + 24 \) = 44 Ω #.
Solution - Method 2
The expression for the total resistance \( R_{\mathrm{T}} \) can be constructed by direct inspection of the circuit, and knowledge of parallel circuits with identical resistances.
\( R_{\mathrm{T}} = 10 \parallel 10 + 15 + 48 \parallel 48 = 5 + 15 + 24 \) = 44 Ω #.
Question 8
The circuit is shown below.
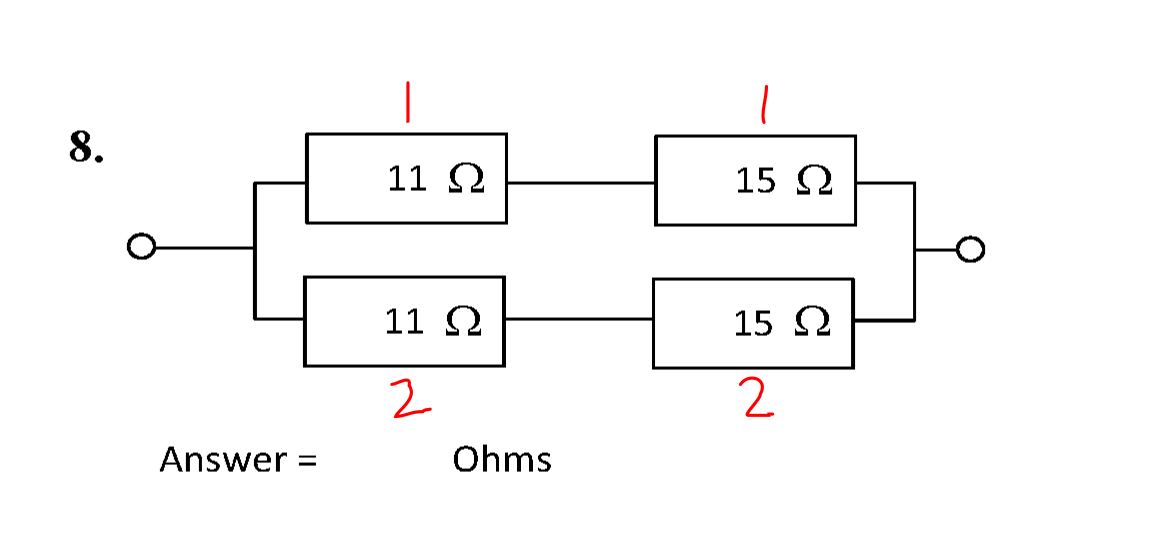
This circuit is a mixed series and parallel circuit. The resistors are grouped into sets that can be treated like individual series or parallel resistors.
Solution
In order to combine the resistors, the series resistances of groups 1 (\( R_1 \)) and 2 (\( R_2 \)) must be calculated. Notice that \( R_1 \) and \( R_2 \) have the same series resistance.
- \( R_1 = 11 + 15 \) = 26 Ω.
- \( R_2 = R_1 \) = 26 Ω.
The circuit then becomes as below.
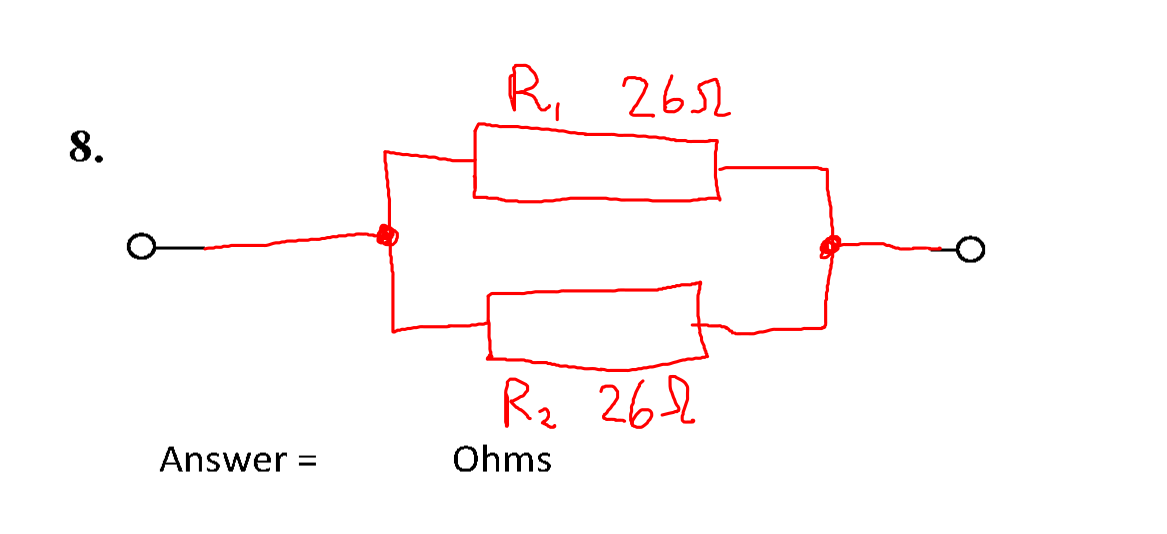
The problem may now be solved as a simple parallel circuit with two identical resistances.
\( R_{\mathrm{T}} = \frac{R_1}{2} = \frac{26}{2} \) = 13 Ω #.
Solution - Method 2
The expression for the total resistance \( R_{\mathrm{T}} \) can be constructed by direct inspection of the circuit, and knowledge of parallel circuits with identical resistances.
\( R_{\mathrm{T}} = (11 + 15) \parallel (11 + 15) \).
NOTE: The parallel operator does not "distribute" the may that multiplication or division does!
In order to go further, the expressions in brackets must be evaluated. Once this is done, the calculation is trivial.
\( R_{\mathrm{T}} = (11 + 15) \parallel (11 + 15) = 26 \parallel 26 = \frac{26}{2} \) = 13 Ω #.
Question 9
The circuit is shown below.
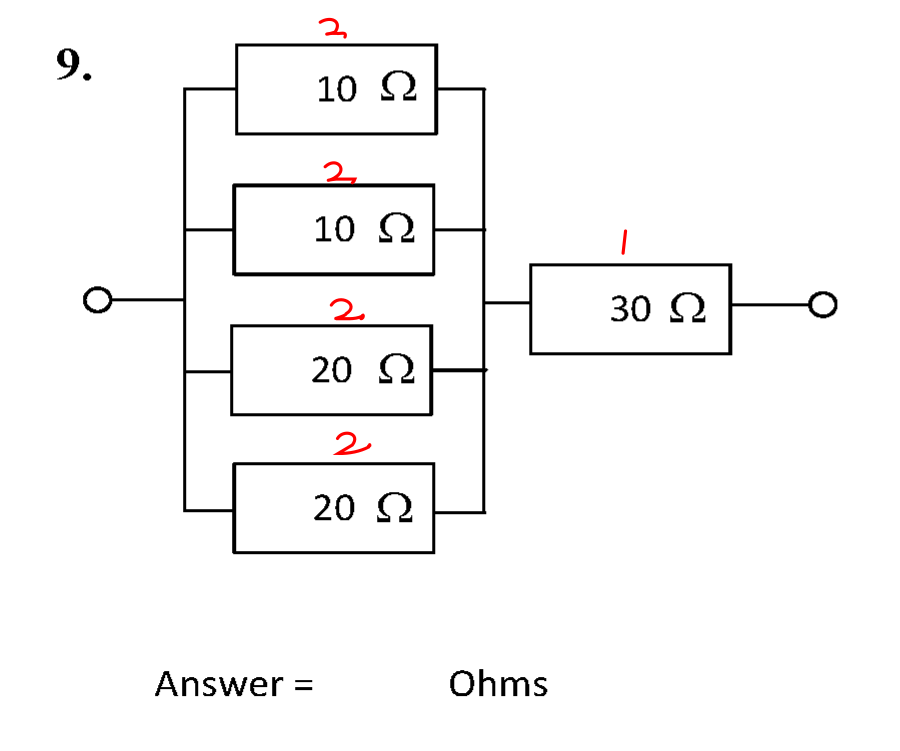
This circuit is a mixed series and parallel circuit. The resistors are grouped into sets that can be treated like individual series or parallel resistors.
Solution
In order to combine the resistors, the series resistance of group 2 (\( R_2 \)) must be calculated.
- \( R_1 = \left( \frac{1}{10} + \frac{1}{10} + \frac{1}{20} + \frac{1}{20} \right)^{-1} = \left( \frac{3}{10} \right)^{-1} = \frac{10}{3}\) Ω.
The circuit then becomes as below.
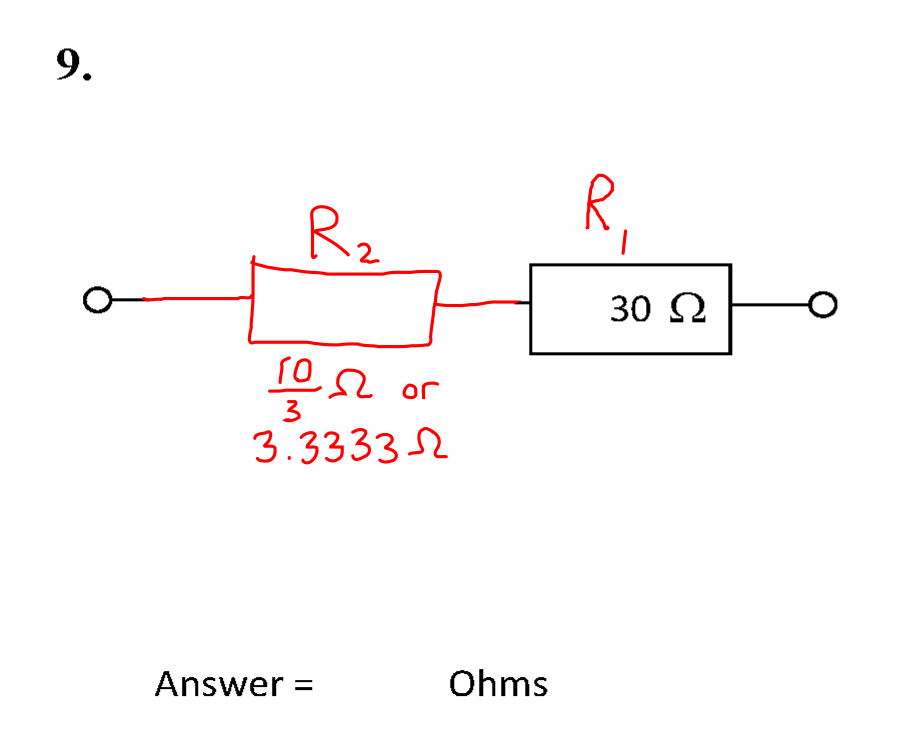
The problem may now be solved as a simple series circuit.
\( R_{\mathrm{T}} = R_1 + R_2 = 30 + \frac{10}{3} = \frac{100}{3} \) = 33.3 Ω (3 sf) #.
Solution - Method 2
The expression for the total resistance \( R_{\mathrm{T}} \) can be constructed by direct inspection of the circuit, and knowledge of parallel circuits with identical resistances.
\( R_{\mathrm{T}} = 10 \parallel 10 \parallel 20 \parallel 20 + 30 = 10 \parallel 10 \parallel (20 \parallel 20) + 30 = 10 \parallel 10 \parallel 10 + 30 = 30 + \frac{10}{3} \) = 33.3 Ω (3 sf) #.