Worksheet 10A - Total Resistance Network - Solutions and Commentary
General Notes
These questions are all concern pure series resistance circuits.
The general formula for the total resistance \( R_{\mathrm{T}} \) of series resistance circuit is shown below.
The general formula is:
\( R_{\mathrm{T}} = \sum R \)
where \( R_{\mathrm{T}} \) is the total series resistance, the sum symbol \( \sum \) represents a summation, and \( R \) is a resistor in the series circuit.
Question 1
The circuit is shown below.

Solution
The total resistance \( R_{\mathrm{T}} \) is simply the sum of the individual resistances.
\( R_{\mathrm{T}} = \sum R = 5 + 5 + 12 + 16 + 8 \) = 46 Ω #.
Question 2
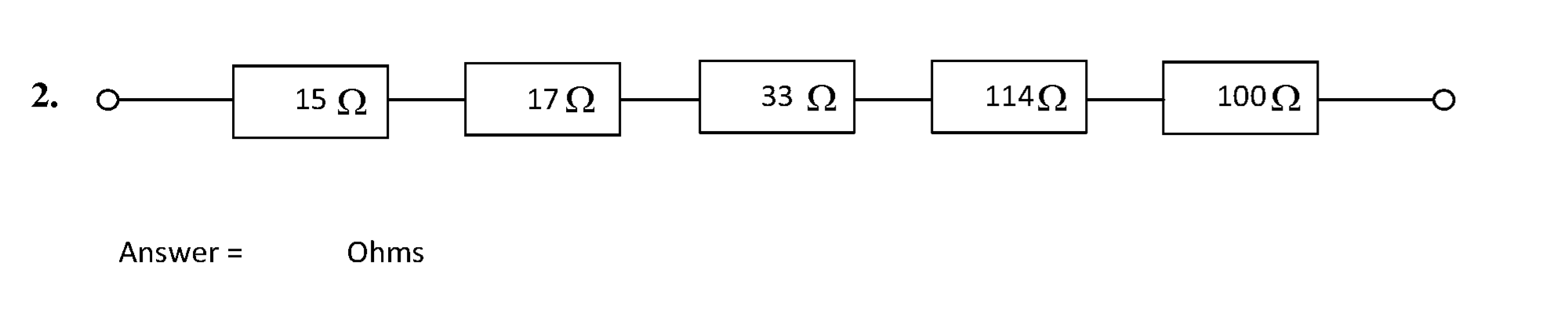
The circuit is shown below.
Solution
The total resistance \( R_{\mathrm{T}} \) is simply the sum of the individual resistances.
\( R_{\mathrm{T}} = \sum R = 15 + 17 + 33 + 114 + 100 \) = 279 Ω #.
Question 3
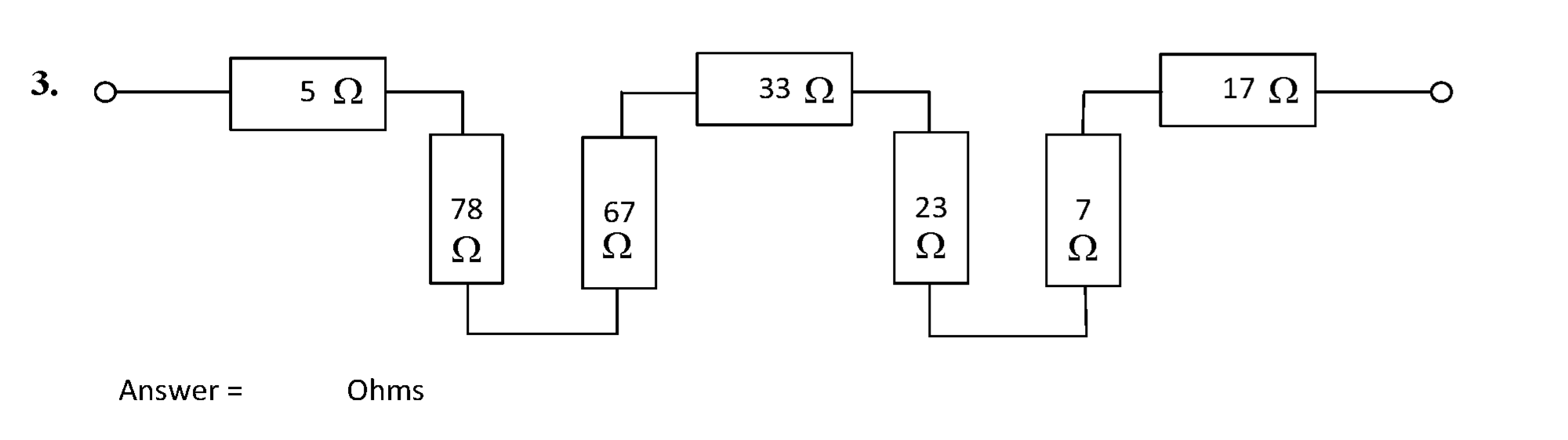
The circuit is shown below.
Solution
This solution traverses the circuit from left to right. Take care that you don't skip over any components.
The total resistance \( R_{\mathrm{T}} \) is simply the sum of the individual resistances.
\( R_{\mathrm{T}} = \sum R = 5 + 78 + 67 + 33 + 23 + 7 + 17 \) = 230 Ω #.
Question 4
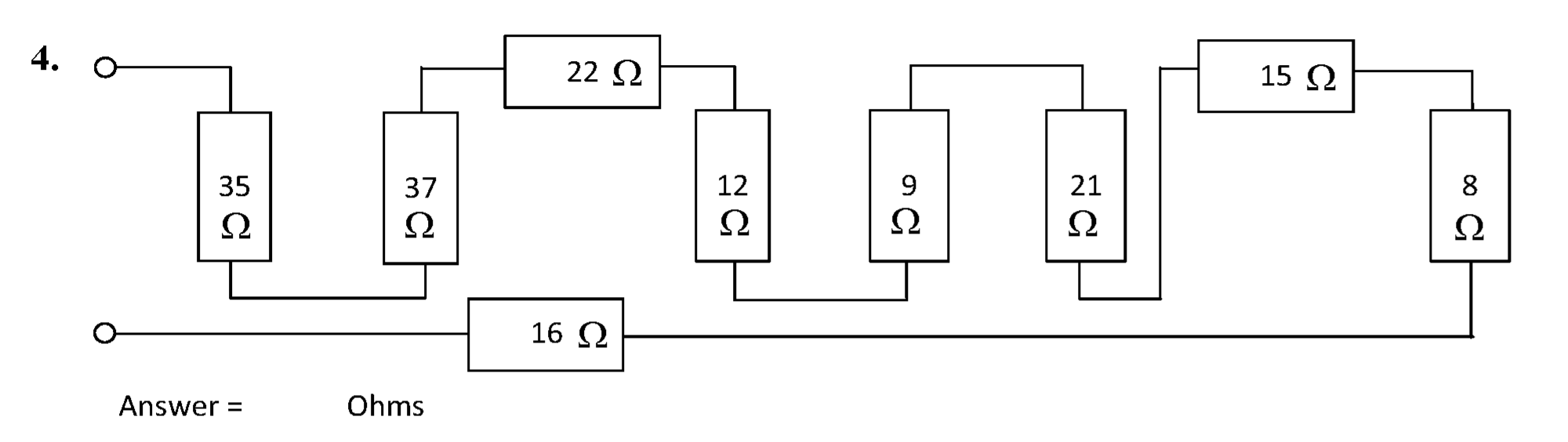
The circuit is shown below.
Solution
This solution traverses the circuit clockwise, from the 'top' terminal to the 'bottom' terminal. Take care that you don't skip over any components.
The total resistance \( R_{\mathrm{T}} \) is simply the sum of the individual resistances.
\( R_{\mathrm{T}} = \sum R = 35 + 37 + 22 + 12 + 9 + 21 + 15 + 8 + 16 \) = 175 Ω #.
Question 5
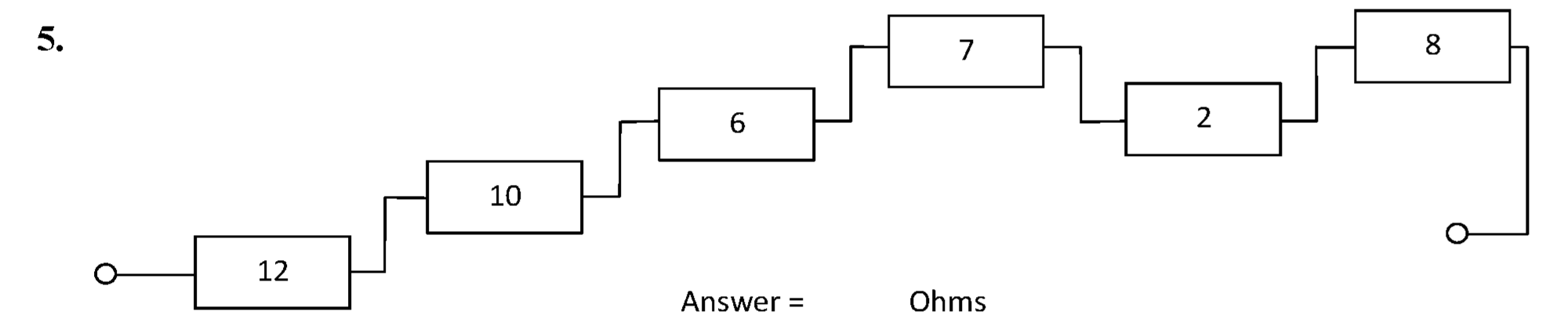
The circuit is shown below.
Solution
This solution traverses the circuit left to right. Take care that you don't skip over any components.
The total resistance \( R_{\mathrm{T}} \) is simply the sum of the individual resistances.
\( R_{\mathrm{T}} = \sum R = 12 + 10 + 6 + 7 + 2 + 8 \) = 45 Ω #.
Question 6
The circuit is describes of consisting of the following resistors in series: six 15 Ω, three 10 Ω, and two 8 Ω resistors. The objective is to calculate the total resistance \( R_{\mathrm{T}} \).

Solution
- The total resistance of a set of series resistors does not depend on the order of the resistors in the series circuit.
The total series resistance can be calculated the same as any other series circuit.
\( R_{\mathrm{T}} = \sum R = 6 \cdot 15 + 3 \cdot 10 + 2 \cdot 8 = 90 + 30 + 16 \) = 136 Ω #.
An example schematic is shown below. The schematic must show the resistors as being connected in series.
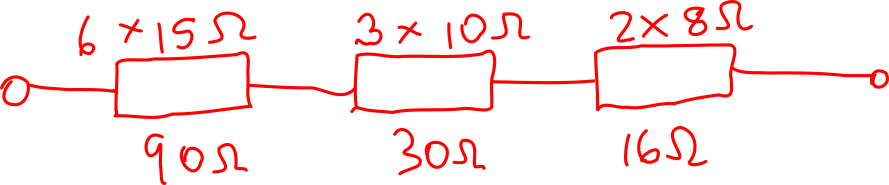
There is little point drawing every single resistor, as the series resistance is the same in any case.