Worksheet 10C - Total Resistance Network - Solutions and Commentary
Question 1
The circuit is shown below.
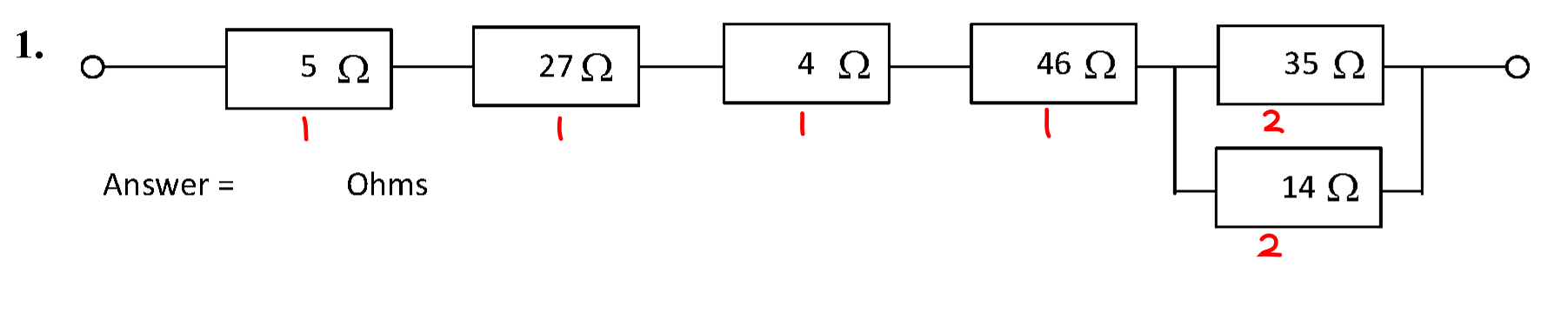
The resistors are grouped up into two groups 1, and 2.
Solution
The total resistance \( R_{\mathrm{T}} \) is simply the sum of \( R_1 \) and \( R_2 \).
\( R_1 \) is the total of all the series resistors. \( R_2 \) is the total of all the parallel resistors.
- \( R_1 = 5 + 27 + 4 + 46 \) = 82 Ω.
- \( R_2 = \left ( 35^{-1} + 14^{-1} \right )^{-1} \) = 10 Ω.
The updated circuit is shown below.

The total resistance \( R_{\mathrm{T}} \) is simply the sum of \( R_1 \) and \( R_2 \).
\( R_{\mathrm{T}} = R_1 + R_2 = 82 + 10 \) = 92 Ω #.
Question 2
The circuit is shown below.
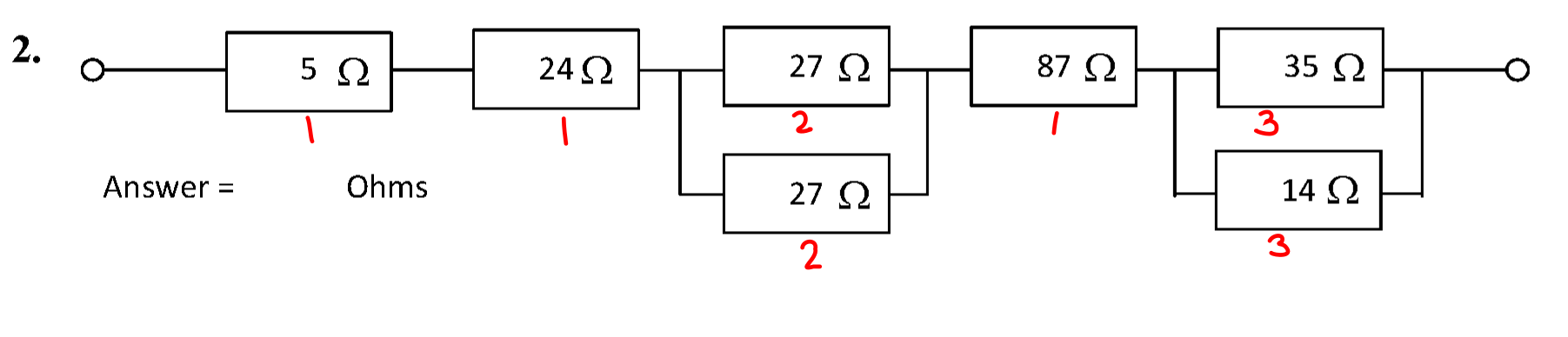
The resistors are grouped up into three groups 1-3.
The order of resistors in a series circuit does not matter, even if they are "separated" by parallel circuits. It is ok to group the 87 ohm resistor in with the 5 ohm and 24 ohm resistors.
Solution - Method 1
The total resistance \( R_{\mathrm{T}} \) is simply the sum of \( R_1 \), \( R_2 \) and \( R_3 \).
- \( R_1 = 5 + 24 + 87 \) = 116 Ω.
- \( R_2 = \frac{27}{2} \) = 13.5 Ω.
- \( R_3 = \left ( 35^{-1} + 14^{-1} \right )^{-1} \) = 10 Ω.
The new equivalent circuit is shown below.
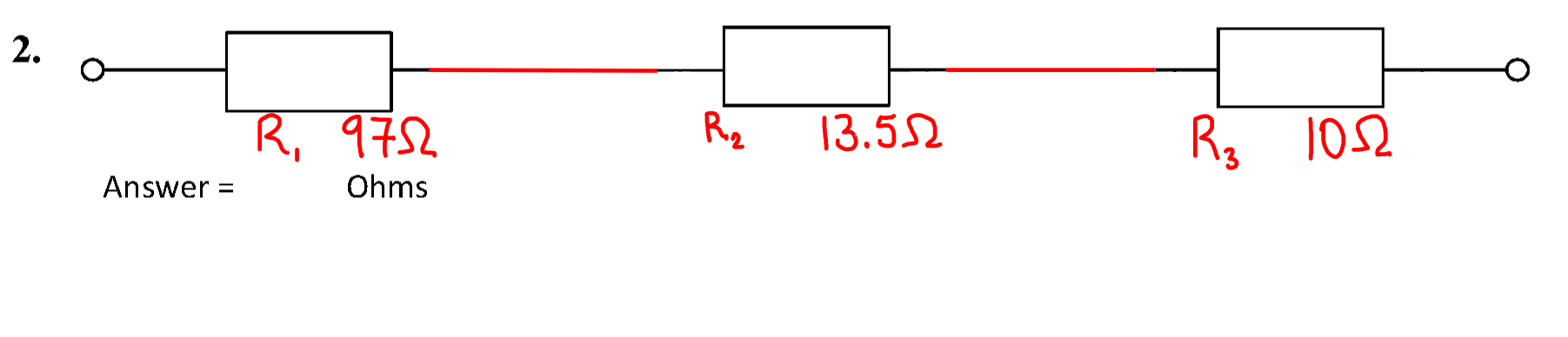
The total resistance \( R_{\mathrm{T}} \) is simply the sum of the individual series resistors.
\( R_{\mathrm{T}} = R_1 + R_2 + R_3 = 116 + 13.5 + 10 \) = 139.5 Ω #.
Solution - Method 2
The total resistance \( R_{\mathrm{T}} \) can be calculated by direct inspection of the circuit.
\( R_{\mathrm{T}} = 5 + 24 + 87 + 27 \parallel 27 + 35 \parallel 14 \)
\( R_{\mathrm{T}} = 116 + 13.5 + 10 \)
\( R_{\mathrm{T}} \) = 139.5 Ω #.
Question 3
The circuit is shown below.

The resistors are grouped as shown.
The right hand part of the network is made up of resistors connected in a way that makes their resistance equal to the left hand side.
Solution
The total resistance is equal to twice the series combination of \( R_1 \) and \( R_2 \) i.e. \( R_{\mathrm{T}} = 2 \cdot ( R_1 + R_2 ) \).
First, we calculate \( R_1 \).
\( R_1 = \left( 36^{-1} + 45^{-1} \right)^{-1} \) = 20 Ω.
The new equivalent circuit is shown below.

The total resistance \( R_{\mathrm{T}} \) can be calculated below.
\( R_{\mathrm{T}} = 2 \cdot (20 + 10) \) = 60 Ω #.
Question 4
The circuit is shown below.
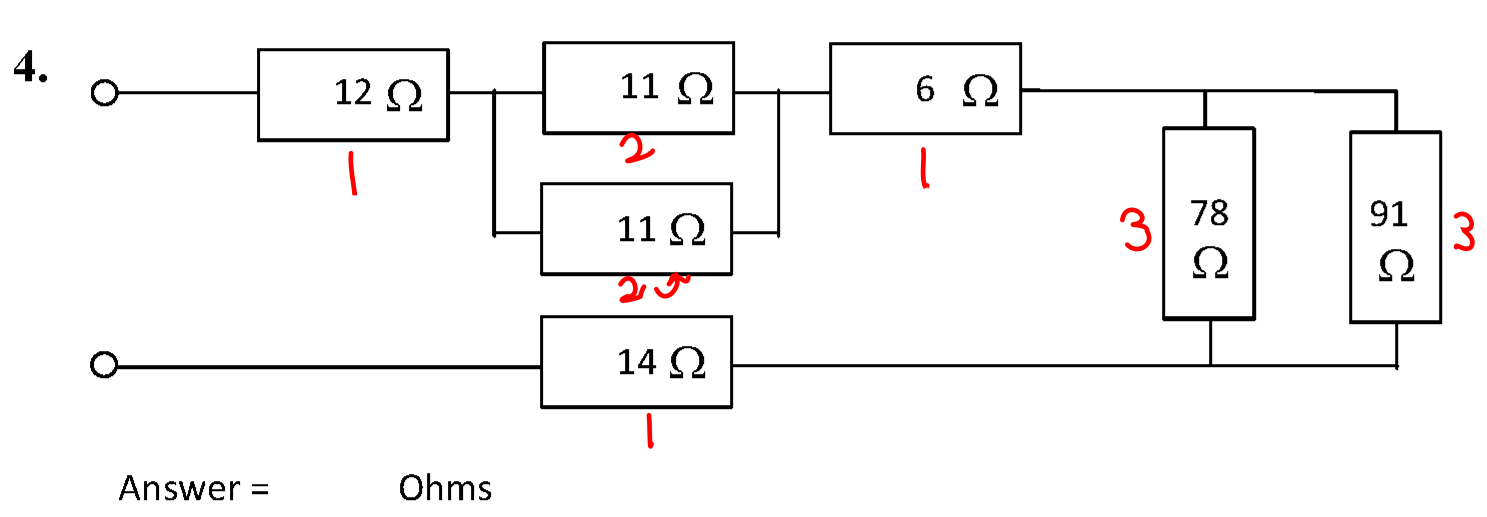
The groupings are as shown. There are a total of three groups.
Solution - Method 1
The equation for the total resistance \( R_{\mathrm{T}} is shown below.
\( R_{\mathrm{T}} = R_1 + R_2 + R_3 \).
We need to solve for \( R_1 \), \( R_2 \) and \( R_3 \).
- \( R_1 = 12 + 6 + 14 \) = 32 Ω.
- \( R_2 = \frac{11}{2} \) = 5.5 Ω.
- \( R_3 = (78^{-1} + 91^{-1})^{-1} \) = 42 Ω.
The new equivalent circuit is shown below.

We have values for \( R_1 \), \( R_2 \) and \( R_3 \), so we can calculate \( R_{\mathrm{T}}.
\( R_{\mathrm{T}} = R_1 + R_2 + R_3 = 32 + 5.5 + 42 \) = 79.5 Ω #.
Question 5
The circuit is shown below.

The groupings are as shown. There are a total of two groups.
NOTE: The total resistance of \( n \) identical resistors of value \( R \) in series is \( R_{\mathrm{T}} = n R \).
Solution
The equation for the total resistance \( R_{\mathrm{T}} is shown below.
\( R_{\mathrm{T}} = R_1 + R_2 \).
We need to solve for \( R_1 \), \( R_2 \) and \( R_3 \).
- \( R_1 = 6 \cdot 19 \) = 114 Ω.
- \( R_2 = \frac{19}{2} \) = 9.5 Ω.
The new equivalent circuit is shown below.

We have values for \( R_1 \) and \( R_2 \), so we can calculate \( R_{\mathrm{T}}.
\( R_{\mathrm{T}} = R_1 + R_2 = 114 + 9.5 \) = 123.5 Ω #.
Question 6
The question is shown below, with the equivalent circuit.
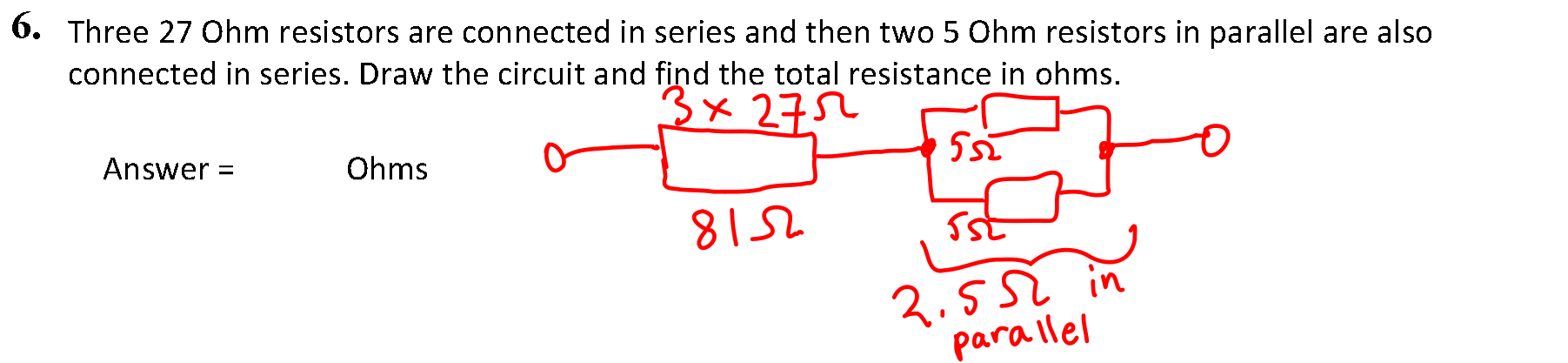
Solution
The solution has been "pre-worked" as shown above.
The total resistance is 81 + 2.5 = 83.5 Ω.